Question

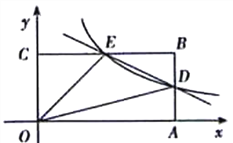
【题目】如图，Rt△ABE中，AB⊥AE以AB为直径作⊙O，交BE于C，弦CD⊥AB，F为AE上一点，连FC，则FC=FE

（1）求证：CF是⊙O的切线；

（2）已知点P为⊙O上一点，且tan∠APD=，连CP，求sin∠CPD的值．

Answer 1

【答案】(1)证明见解析；（2）

【解析】试题分析：

试题解析：

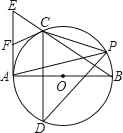
（1）证明：连接OC，

∵AB是直径，

∴∠BAE=90°，

∴∠B+∠E=90°，

又∵OB=OC，CF=EF，

∴∠BCO=∠CBO，∠E=∠ECF，

∴∠BCO+∠ECF=90°，

∴∠FCO=90°，

∴CF是⊙O切线；

（2）解：∵CD⊥AB，

∴ ，

∴∠B=∠APD，∠COM=∠CPD，

∴tan∠APD=tan∠B=，

设CM=t，BM=2t，OB=OC=R，OM=2t﹣R，

∴R2=t2+（2t﹣R）2，

∴R= ，

∴sin∠CPD=sin∠COM=．