题目内容
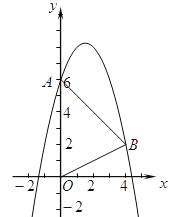
【题目】如图,在平面直角坐标系中,△ABC的顶点坐标为A(﹣4,1),B(﹣2,3),C(﹣1,2).
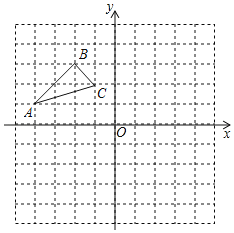
(1)画出△ABC关于原点O成中心对称的△A′B′C′,点A′,B′,C′分别是点A,B,C的对应点.
(2)求过点B′的反比例函数解析式.
(3)判断A′B′的中点P是否在(2)的函数图象上.
【答案】(1)如图,见解析;(2)y=﹣![]() ;(3)点P在(2)的函数图象上.
;(3)点P在(2)的函数图象上.
【解析】
(1)根据关于原点成中心对称的点的坐标特征,即横纵坐标均为相反数,找到对应点,然后依次连线即可.
(2)根据待定系数法,设出反比例函数解析式,然后将B′的坐标代入计算即可.
(3)确定A′B′的中点P的坐标,然后将P点的坐标代入函数解析式,即可解决问题.
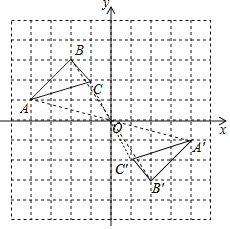
(1)∵A(﹣4,1),B(﹣2,3),C(﹣1,2).
关于原点对称的点的坐标横纵坐标均为相反数
∴A′(4,-1),B′(2,-3),C′(1,-2)
在坐标系中找到A′、B′、C′,依次连线即可.
如图:
(2)设过点B′的反比例函数解析式为y=![]() ,
,
∵B′(2,﹣3),
∴﹣3=![]() ,
,
∴k=﹣6,
∴反比例函数解析式为y=﹣![]() ;
;
(3)∵A′(4,﹣1),B′(2,﹣3)
∴A′B′的中点P坐标为(3,﹣2),
∵3×(﹣2)=﹣6,
∴点P在(2)的函数图象上.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目