Question

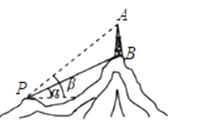
【题目】如图，一条高速公路在城市A的东偏北30°方向直线延伸，县城M在城市A东偏北60°方向上，测验员从A沿高速公路前行4000米到达C，测得县城M位于C的北偏西60°方向上，现要设计一条从县城M进入高速公路的路线，请在高速公路上寻找连接点N，使修建到县城M的道路最短，试确定N点的位置并求出最短路线长．（结果取整数，≈1.732）

Answer 1

【答案】解：如图，过M作MN⊥AC交于N点，即MN最短，
∵∠EAD=60°，∠CAD=30°，
∴∠CAM=30°，
∴∠AMN=60°，
又∵C处看M点为北偏西60°，
∴∠FCM=60°，
∴∠MCB=30°，
∵∠EAC=60°，
∴∠CAD=30°，
∴∠BCA=30°，
∴∠MCA=∠MCB+∠BCA=60°，
∴在Rt△AMC中，∠AMC=90°，∠MAC=30°，
∴MC=AC=2000，∠CMN=30°，
∴NC=MC=1000，
∵AC=4000米，
∴AN=AC﹣NC=4000﹣1000=3000（米）．
答：点N到A市最短路线3000米．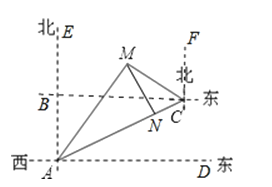

【解析】过M作MN⊥AC交于N点，即MN最短，根据方向角可以证得∠AMC=90°，根据三角函数即可求得MC，进而求得AN的长．
【考点精析】解答此题的关键在于理解解直角三角形的相关知识，掌握解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)．