Question

【题目】在一山顶有铁塔AB，从点P到铁塔底部B点有一条索道PB，索道长为300米，与水平线成角为α=30°，在P处测得A点的仰角为β=45°，试求铁塔的高AB．（精确到0.1米，其中≈1.41，≈1.73）

Answer 1

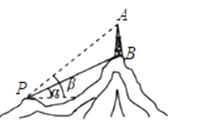
【答案】解：由题意得，PB=300米，∠BPC=30°，
∴BC=PBsin∠BPC=150米，PC=PBcos∠BPC=150≈259.5米，
∵∠APC=45°，
∴AC=PC=259.5米，
∴AB=AC﹣BC=109.5米．
答：铁塔的高AB约为109.5米．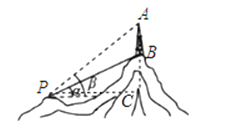

【解析】根据正弦、余弦的定义分别求出BC、PC的长，根据AB=AC﹣BC计算即可．
【考点精析】解答此题的关键在于理解解直角三角形的相关知识，掌握解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)．