题目内容
【题目】如图，在正方形ABCD中 ，AB=1，E，F分别是边BC，CD上
的点，连接EF、
、AF，过A作AH⊥EF于点H. 若
，
那么下列结论：①
平分
；②FH=FD；③∠EAF=45°；
④
； ⑤△CEF的周长为2.
其中正确结论的个数是
A.2 B.3 C.4 D.5
【答案】D
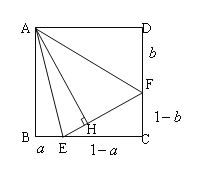【解析】此题考直角三角形全等的判定定理和性质定理的应用、勾股定理的应用、三角形周长和面积的计算、整式的化简与运算等综合知识，属于难题；考查学生的综合运用知识解决问题的能力和逻辑推理论证能力；如图所示
设
，由已知得
；因为
，所以
，所以
，所以
，即
平分
，所以①正确；同理
，且
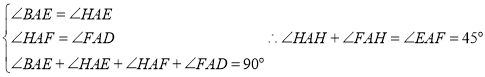，所以②③正确；因为
，即④正确； 由前面可知：△CEF的周长为
，所以⑤正确， 所以选D；
练习册系列答案
相关题目
【题目】为提升学生的艺术素养，某校计划开设四门选修课程：声乐、舞蹈、书法、摄影．要求每名学生必须选修且只能选修一门课程，为保证计划的有效实施，学校随机对部分学生进行了一次调查，并将调査结果绘制成如下不完整的统计表和统计图．
学生选修课程统计表
课程 | 人数 | 所占百分比 |
声乐 | 14 |
|
舞蹈 | 8 |
|
书法 | 16 |
|
摄影 |
|
|
合计 |
|
|
根据以上信息，解答下列问题：
（1）
，
．
（2）求出
的值并补全条形统计图．
（3）该校有1500名学生，请你估计选修“声乐”课程的学生有多少名．
（4）七（1）班和七（2）班各有2人选修“舞蹈”课程且有舞蹈基础，学校准备从这4人中随机抽取2人编排“舞蹈”在开班仪式上表演，请用列表法或画树状图的方法求所抽取的2人恰好来自同一个班级的概率．
