Question

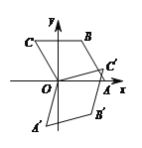
【题目】如图，在同一平面内，将两个全等的等腰直角三角形摆放在一起（如图1），点A为公共顶点，∠BAC＝∠AED＝90°，它们的斜边长为2．若△ABC固定不动，把△ADE绕点A旋转到如图2的位置时，AD、AE与边BC的交点分别为M、N（点M不与点B重合，点N不与点C重合）．

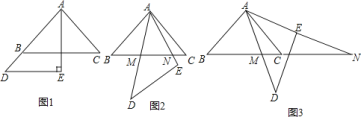
（1）证明：△BAN∽△CMA；

（2）求BNCM的值；

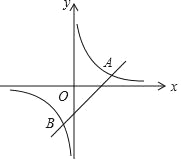
（3）当△ADE绕点A继续旋转到如图3的位置时，AD交BC于点M，AE、BC的延长线交于点N，此时BNCM的值是否发生变化？请你说明理由．

Answer 1

【答案】（1）证明见详解；（2）BNCM=2；（3）不变，理由见详解.

【解析】

（1）由题意可得∠BAN=∠BAD+45°，∠CMA=∠BAD+45°，即可证得∠BAN=∠CMA，又由∠B=∠C=45°，即可证得△BAN∽△CMA；

（2）由△BAN∽△CMA，根据相似三角形的对应边成比例，即可求得BNCM的值；

（3）由∠BAN=∠BAD+45°，∠CMA=∠BAD+45°，即可证得∠BAN=∠CMA，又由∠B=∠ACM=45°，即可证得△BAN∽△CMA，然后由相似三角形的对应边成比例，证得结论．

解：（1）证明：∵∠BAN=∠BAD+45°，∠CMA=∠BAD+45°，

∴∠BAN=∠CMA，

又∵∠B=∠C=45°，

∴△BAN∽△CMA；

（2）解：∵△BAN∽△CMA，

∴BN：CA=BA：CM，

∵斜边长为2，

∴AC=AB=，

∴BNCM=ABAC=2；

（3）解：不变．

理由：∵∠BAN=∠BAD+45°，∠CMA=∠BAD+45°，

∴∠BANE=∠CMA，

又∵∠B=∠ACM=45°，

∴△BAN∽△CMA，

∴BN：CA=BA：CM，

∵AC=AB=，

∴BNCM= ABAC=2．