题目内容
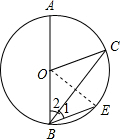
如图，AB是⊙O的直径，E是⊙O上的一点，
的度数为40°，过点O作OC∥BE交⊙O于点C，求∠BCO的度数．
 |
| BE |
连接OE，
∵
的度数为40°，
∴∠BOE=40°，
∵OB=OE，
∴∠OBE=∠OEB=（180°-40°）÷2=70°，
∵OC∥BE，
∴∠C=∠1，
∵CO=BO，
∴∠2=∠C，
∴∠1=∠2，
∴∠BCO=∠1=
∠OBE=35°．
∵
|
| BE |
∴∠BOE=40°，
∵OB=OE，
∴∠OBE=∠OEB=（180°-40°）÷2=70°，
∵OC∥BE，
∴∠C=∠1，
∵CO=BO，
∴∠2=∠C，
∴∠1=∠2，
∴∠BCO=∠1=
| 1 |
| 2 |
练习册系列答案
七星图书口算速算天天练系列答案
初中学业考试导与练系列答案
相关题目
