题目内容
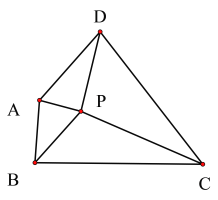
【题目】如图，四边形ABCD中，∠A、∠B 、∠C、 ∠D 的角平分线恰相交于一点P，记作△APD、△APB、△BPC、△DPC的面积分别为
、
、
、
则下列关系式正确的是（ ）
A.
B.
C.
D.
【答案】A
【解析】
由条件可知P为四边形ABCD的内切圆的圆心，作出该圆，分别作出P到各边的距离，可把四边形分为八个三角形，再利用面积和可得△APD、△APB、△BPC、△DPC面积之间的关系.
解：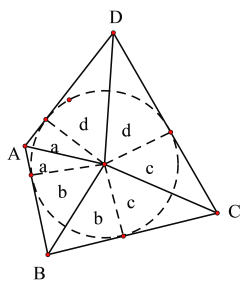
四边形ABCD，∠A、∠B 、∠C、 ∠D 的角平分线恰相交于一点P，则P是该四边形内切圆的圆心，
如图，可将四边形分成8个三角形，面积分别为a、a、b、b、c、c、d、d
则
=a+d 
=a+b 
=b+c 
=c+d
∴+=a+b+c+d=+
故选 A
练习册系列答案
阅读快车系列答案
相关题目
