题目内容
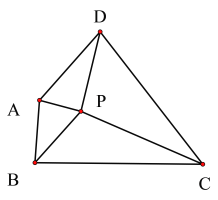
【题目】如图，钝角
的面积为12，最长边
，
平分
，点
、
分别是、
上的动点，则
的最小值是__________．
【答案】3
【解析】
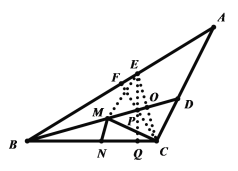
如图（见解析），先根据等腰三角形的判定定理与性质得出
，从而将所求问题转化为求直线外一点到已知直线的最短距离，确认EQ即为最小值，再利用三角形的面积公式求解即可.
如图，过点C作
，延长CO交AB于点E，连接EM
平分
既是
的角平分线，也是高
是等腰三角形，且
，BO是CE的垂直平分线
因此，求
的最小值，也就是求点E到BC的最短距离
过点E作
，交BD于点P，则当点P与点M、点Q与点N分别重合时，
取得最小值，最小值为
（两点之间线段最短、垂线段最短）
再过点C作
在等腰中，由面积公式可得
又
，解得
则的最小值为3，即的最小值为3
故答案为：3.
练习册系列答案
名校课堂系列答案
相关题目
