题目内容
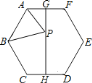
【题目】如图,已知正六边形![]() 的边长为
的边长为![]() ,
,![]() ,
,![]() 分别是
分别是![]() 和
和![]() 的中点,
的中点,![]() 是
是![]() 上的动点,连接
上的动点,连接![]() ,
,![]() ,则
,则![]() 的最小值为( )
的最小值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
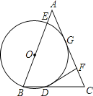
易知点B关于GH的对称点为点E,连接AE交GH于点P,那么有PB=PE,AP+BP=AE最小.又易知△AEF为等腰三角形,∠AFE=120°,则作FM⊥AE于点M,易求得AM=EM=![]() ,从而AE=2
,从而AE=2![]() .
.
利用正多边形的性质可得点B关于GH的对称点为点E,连接AE交GH于点P,那么有PB=PE,AP+BP=AE最小.
又易知△AEF为等腰三角形,∠AFE=120°,
则作FM⊥AE于点M,如图所示:

∵∠AFE=120°,AF=EF,
∴∠FAE=∠FEA=30°,AM=EM,
在RT△AFM中,AF=2,
∴AM=![]() AF=
AF=![]() ,
,
∴AM=EM=![]() ,从而AE=2
,从而AE=2![]() ,
,
故AP+BP的最小值为2![]() .
.
故选:D.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目