题目内容
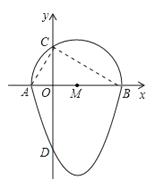
【题目】如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A、B、C、D分别是“果圆”与坐标轴的交点,抛物线的表达式为y=![]() x2-2x-6,AB为半圆的直径,则这个“果圆”被y轴截得的“弦”CD的长为________.
x2-2x-6,AB为半圆的直径,则这个“果圆”被y轴截得的“弦”CD的长为________.

【答案】2![]() +6
+6
【解析】
将x=0代入抛物线的解析式得y=-6,故此可得到DO的长,然后令y=0可求得点A和点B的坐标,故此可得到AB的长,由M为圆心可得到MC和OM的长,然后依据勾股定理可求得OC的长,最后依据CD=OC+OD求解即可.
连接AC,BC.
∵抛物线的解析式为y=![]() x2-2x-6,
x2-2x-6,
∴点D的坐标为(0,-6),
∴OD的长为6.
设y=0,则0=![]() x2-2x-6,解得:x=-2或6,
x2-2x-6,解得:x=-2或6,
∴A(-2,0),B(6,0).
∴AO=2,BO=6,AB=8,M(2,0).
∴MC=4,OM=2.
在Rt△COB中,OC=![]() ,
,
∴CD=CO+OD=6+2![]() ,即这个“果圆”被y轴截得的线段CD的长6+2
,即这个“果圆”被y轴截得的线段CD的长6+2![]() .
.
故答案为:6+2![]()

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目