题目内容
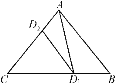
【题目】定义:若经过三角形顶点的一条直线把三角形分割出至少一个图形与原三角形相似,则称这条直线为三角形的自似线,如图,△ABC中,AC=b,BC=a,∠C<∠B<∠A,过顶点A作∠CAD1=∠B,交边BC于点D1,依次过顶点D1作∠CD1D2=∠CAD1,过点D2作∠CD2D3=∠CD1D2,…,过点Dn-1作∠CDn-1Dn=∠CDn-2Dn-1.
(1)试证直线AD1是△ABC的自似线;
(2)试求线段CD1的长,并猜想CDn的长;
(3)当60°<∠A<120°,且n=5时,与△ABC相似的三角形有几个?
【答案】(1)证明见解析;(2) CD1=![]() ,
, ![]() ;(3)当∠ A=90°时,与△ABC相似的三角形有10个;当∠ A≠90°时,与△ABC相似的三角形有5个.
;(3)当∠ A=90°时,与△ABC相似的三角形有10个;当∠ A≠90°时,与△ABC相似的三角形有5个.
【解析】
(1)由∠C=∠ C,∠CAD1=∠ B,得△CAD1∽△CBA,即直线AD1是△ABC的自似线.
(2)由(1)得△CAD1∽△CBA,![]() , 可得CD1=
, 可得CD1=![]() ,
,![]() .
.
(3)画图可知当∠ A=90°时,与△ABC相似的三角形有10个;当∠ A≠90°时,与△ABC相似的三角形有5个.
(1)证明:∵∠C=∠ C,∠CAD1=∠ B,
∴△CAD1∽△CBA,
∴直线AD1是△ABC的自似线.
(2)由(1)得△CAD1∽△CBA,
∴![]() ,
,
∴CD1=![]() ,
, ![]() .
.
(3)当∠ A=90°时,与△ABC相似的三角形有10个;当∠ A≠90°时,与△ABC相似的三角形有5个.

练习册系列答案
相关题目