题目内容
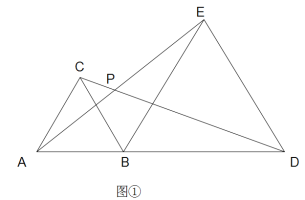
【题目】在四边形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB上一点,AE=AD,且BF∥CD,AF⊥CE的延长线于F.连接DE交对角线AC于H.下列结论:①△ACD≌ACE;②AC垂直平分ED;③CE=2BF;④CE平分∠ACB.其中结论正确的是________.(填序号)

【答案】①②③④
【解析】
由已知条件可直接证得△ACD≌△ACE;由三角形全等的性质可得CD=CE,又因为AD=AE所以AC是DE的垂直平分线即AC垂直平分ED;延长AF,CB相交于点G,证出△ABG≌△CBE,则AG=CE=CD,再证出AG=2BF即可得出③正确;取CE的中点I连接BI,可得CE=2BI,再证明BF=BI,再利用三角形的外角性质和平行线的性质问题④可得证.
解:①∵AD∥BC,∠ABC=90°,
∴∠BAD=90°.
∵AB=CB,
∴∠BAC=45°,
∴∠DAC=45°.
又∵AC=AC,AE=AD,
∴△AEC≌△ADC.
故①正确.
②∵△AEC≌△ADC,
∴DC=CE.
又∵AD=AE,
∴AC是DE的垂直平分线.
即AC垂直平分ED.
故②正确.
③延长AF,CB相交于点G,则∠ABG=∠ABC=90°,

∵∠BEC+∠BCE=90°,
又∵AF⊥CE,
∴∠AEF+∠BAG=90°,
∵∠BEC=∠AEF,
∴∠BCE=∠BAG,
又∵AB=BC,
∴△ABG≌△CBE,
∴AG=CE=CD,
又∵AD//BC,
∴∠G=∠DCG,
∵BF//CD,
∴∠DCG=∠FBG,
∴∠G=∠FBG,
∴BF=FG.
又∵∠ABG=90°,
∴AG=2BF.
即CE=2BF.
故③正确;
④取CE的中点I,连接BI,则BI=CI=EI.

∴∠CBI=∠BCI,
∴∠BIF=2∠BCI.
∵CE=2BF,
∴BF=BI,
∴∠BFI=∠BIF=2∠BCI.
∵BF//CD,
∴∠BFI=∠DCE,
∴∠BCI=![]() ∠DCE=∠ACE,
∠DCE=∠ACE,
∴CE平分∠ACB.
故④正确.
故答案为:①②③④.