题目内容
【题目】探究:
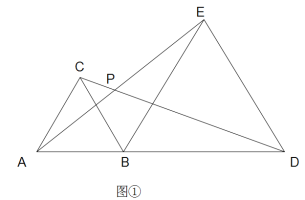
(1)如图1,在△ABC与△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°,连结BD、CE.请写出图1中所有全等的三角形: (不添加字母).
(2)如图2,已知△ABC,AB=AC,∠BAC=90°,![]() 是过A点的直线,CN⊥
是过A点的直线,CN⊥![]() ,BM⊥
,BM⊥![]() ,垂足为N、M.求证:△ABM≌△CAN.
,垂足为N、M.求证:△ABM≌△CAN.
解决问题:
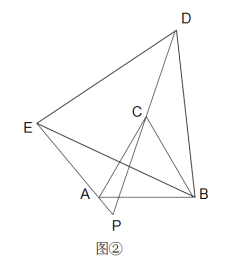
(3)如图3,已知△ABC,AB=AC,∠BAC=90°,D在边BC上,DA=DE,∠ADE =90°.
求证:AC⊥CE.

【答案】(1)△ABD≌△ACE;(2)见详解;(3)见详解.
【解析】
(1)由∠DAB+∠BAE=∠BAE+∠EAC=90°,得到∠DAB=∠EAC,然后结合AB=AC,AD=AE,即可证明△ABD≌△ACE;
(2)由同角的余角相等,得到∠BAM=∠CAN,结合条件AB=AC,∠AMB=∠ANC=90°,即可证明△ABM≌△CAN;
(3)作AH⊥BC于H,EG⊥BC于G,由△ABC是等腰直角三角形,则AH=BH=CH,由∠DAH=∠EDG,得到△ADH≌△DEG,则DG=AH=CH,DH=EG,则DH+HG=HG+GC,得到EG=CG,则得到∠ECG=45°,则∠ACE=90°,即可得到结论成立.
证明:(1)∵∠DAB+∠BAE=∠DAE=90°,∠BAE+∠CAE=∠BAC=90°,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
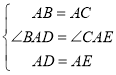 ,
,
∴△ABD≌△ACE(SAS);
故答案为:△ABD≌△ACE;
(2)∵∠CAN+∠ACN=90°,∠CAN+∠BAM=90°,
∴∠ACN=∠BAM,
在△ABM和△CAN中,
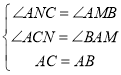 ,
,
∴△ABM≌△CAN(AAS);
(3)如图:作AH⊥BC于H,EG⊥BC于G,则∠AHD=∠DGE=90°,
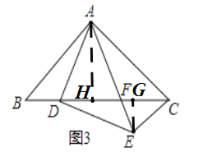
∵△ABC是等腰直角三角形,
∴AH=BH=CH,∠ACB=45°,
∵∠ADH+∠DAH=∠ADH+∠EDG=90°,
∴∠DAH=∠EDG,
∵AD=DE,
∴△ADH≌△DEG,
∴DG=AH=CH,DH=EG,
∵DH+HG=HG+GC,
∴DH=CG=EG,
∴△CEG是等腰直角三角形,
∴∠ECG=45°,
∴∠ACE=∠ACB+∠ECG=45°+45°=90°,
∴AC⊥CE.

 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案