题目内容
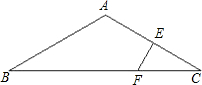
 如图所示,△ABC中,AB=10,AC=8,角平分线BD、CD交于点D,过点D作EF∥BC,交AB于点E,交AC于点F,则△AEF的周长是
如图所示,△ABC中,AB=10,AC=8,角平分线BD、CD交于点D,过点D作EF∥BC,交AB于点E,交AC于点F,则△AEF的周长是
- A.10
- B.8
- C.9
- D.18
D
分析:利用已知给出的平行线及角平分线的性质可得到许多对角是相等的,根据等校对等边的性质可得线段相等,进行等量代换周长可得.
解答: 解:∵EF∥BC,
解:∵EF∥BC,
∴∠2=∠3.
又BD是∠ABC的平分线,
∴∠1=∠3.
∴∠2=∠1.
于是ED=EB.
同理,FD=FC.
△AEF的周长为:(AE+ED)+(AF+FD)=(AE+EB)+(AF+FC)=10+8=18.
故选D.
点评:本题考查了平行线的性质和角平分线的定义几等腰三角形的判定;根据等角对等边,可以将周长转化为三角形两边长,有效的对线段进行转移是正确解答本题的关键.
分析:利用已知给出的平行线及角平分线的性质可得到许多对角是相等的,根据等校对等边的性质可得线段相等,进行等量代换周长可得.
解答:
 解:∵EF∥BC,
解:∵EF∥BC,∴∠2=∠3.
又BD是∠ABC的平分线,
∴∠1=∠3.
∴∠2=∠1.
于是ED=EB.
同理,FD=FC.
△AEF的周长为:(AE+ED)+(AF+FD)=(AE+EB)+(AF+FC)=10+8=18.
故选D.
点评:本题考查了平行线的性质和角平分线的定义几等腰三角形的判定;根据等角对等边,可以将周长转化为三角形两边长,有效的对线段进行转移是正确解答本题的关键.

练习册系列答案
相关题目
 如图所示,△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.求证:BF=2CF.
如图所示,△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.求证:BF=2CF. 16、如图所示,△ABC中,∠C=90°,DE垂直平分斜边AB,分别交AB、AC于D、E,∠CAE:∠EAB=5:2,则∠B=
16、如图所示,△ABC中,∠C=90°,DE垂直平分斜边AB,分别交AB、AC于D、E,∠CAE:∠EAB=5:2,则∠B=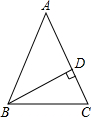 如图所示,△ABC中,AB=AC=10,BD是AC边的高线,DC=2,试求BD的长.
如图所示,△ABC中,AB=AC=10,BD是AC边的高线,DC=2,试求BD的长. 如图所示,△ABC中,BC的垂直平分线交AB于点E,若△ABC的周长为10,BC=4,则△ACE的周长是
如图所示,△ABC中,BC的垂直平分线交AB于点E,若△ABC的周长为10,BC=4,则△ACE的周长是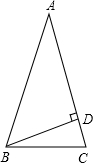 如图所示,△ABC中,AB=AC,BD⊥AC,垂足为D,求∠DBC与∠A的关系.
如图所示,△ABC中,AB=AC,BD⊥AC,垂足为D,求∠DBC与∠A的关系.