题目内容
【题目】如图,已知抛物线y=﹣x2+4x+5与x轴的两个交点为A、B,与y轴交于点C.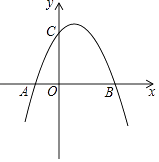
(1)求A,B,C三点的坐标?
(2)求该二次函数的对称轴和顶点坐标?
(3)若坐标平面内的点M,使得以点M和三点A,B,C为顶点的四边形是平行四边形,求点M的坐标?(直接写出M的坐标)
【答案】
(1)
解:对应抛物线y=﹣x2+4x+5,令y=0,得﹣x2+4x+5=0,解得x=﹣1或5,
∴A(﹣1,0),B(5,0),
令x=0得y=5,
∴点C坐标(0,5),
∴A(﹣1,0),B(5,0),C(0,5)
(2)
解:∵y=﹣x2+4x+5=﹣(x2﹣4x)+5=﹣(x﹣2)2+9,
∴对称轴x=2,顶点坐标为(2,9)
(3)
解:如图,满足条件的点有三个,设M1(m,n).
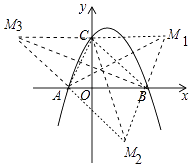
∵四边形ABM1C是平行四边形,
∴BC与AM1互相平分,
∴ ![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
∴m=6,n=5,
∴M1(6,5),同理可得M2(4,﹣5),M3(﹣5,5).
∴满足条件的点M坐标为(6,5)或(4,﹣5)或(﹣5,5)
【解析】(1)对应抛物线分别令y=0,x=0解方程即可.(2)利用配方法即可解决问题.(3)满足条件的点有三个,设M1(m,n).由四边形ABM1C是平行四边形,推出BC与AM1互相平分,可得 ![]() =
= ![]() ,
, ![]() =
= ![]() ,解方程即可解决问题.
,解方程即可解决问题.
【考点精析】本题主要考查了二次函数的概念和二次函数的图象的相关知识点,需要掌握一般地,自变量x和因变量y之间存在如下关系:一般式:y=ax2+bx+c(a≠0,a、b、c为常数),则称y为x的二次函数;二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点才能正确解答此题.

练习册系列答案
相关题目