Question

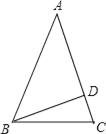
【题目】在等腰△ABC中，已知AB＝AC，BD⊥AC于D．

(1)若∠A＝48°，求∠CBD的度数；

(2)若BC＝15，BD＝12，求AB的长．

Answer 1

【答案】(1)∠CBD＝24°；(2)AB＝．

【解析】

（1）根据等腰三角形的性质和直角三角形的两个锐角互余，可以求得∠CBD的度数；
（2）根据题目中的数据和勾股定理，可以求得AB的长．

解：(1)∵在等腰△ABC中，AB＝AC，BD⊥AC，

∴∠ABC＝∠C，∠ADB＝90°，

∵∠A＝48°，

∴∠ABC＝∠C＝66°，∠ABD＝42°，

∴∠CBD＝24°；

(2)∵BD⊥AC，

∴∠BDC＝90°，

∵BC＝15，BD＝12，

∴CD＝9，

设AB＝x，则AD＝x﹣9，

∵∠ADB＝90°，BD＝12，

∴122+(x﹣9)2＝x2，

解得，x＝，

即AB＝．