Question

【题目】如图，在直角坐标平面中，O为原点，点A的坐标为（20，0），点B在第一象限内，BO＝10，sin∠BOA＝ ．

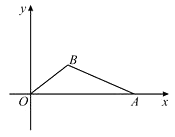
（1）①在图中，求作△ABO的外接圆；（尺规作图，不写作法但需保留作图痕迹）;②求点B的坐标与cos∠BAO的值；
（2）若A，O位置不变，将点B沿 轴正半轴方向平移使得△ABO为等腰三角形，请直接写出平移距离．

Answer 1

【答案】
（1）解：①如图所示：

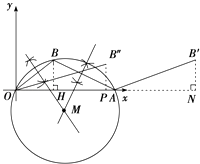
②作BH⊥OA，垂足为H，

在Rt△OHB中，∵BO=10，sin∠BOA= ，

∴BH=6，

∴OH=8，∴点B的坐标为（8，6），

∵OA=20，OH=8，∴AH=12，

在Rt△AHB中，∵BH=6，

∴AB= =6

∴cos∠BAO= =

（2）解：①当BO=AB时，∵AO=20，∴OH=10，

∴点B沿x轴正半轴方向平移2个单位，

②当AO=AB′时，∵AO=20，∴AB′=20，

过B′作B′N⊥x轴，

∵点B的坐标为（8，6），

∴B′N=6，∴AN= =2 ．

∴点B沿x轴正半轴方向平移（2 +12）个单位，

③当AO=OB″时，

∵AO=20，

∴OB″=20，

过B″作B″P⊥x轴．

∵B的坐标为（8，6），

∴B″P=6，

∴OP= =2 ，

∴点B沿x轴正半轴方向平移（2 ﹣8）个单位，

综上所述当点B沿x轴正半轴方向平移2个单位、（2 +12）个单位，或（2 ﹣8）个单位时，△ABO为等腰三角形

【解析】（1）作出BO和AB的垂直平分线，两线交点就是外接圆圆心，以交点为圆心，交点到O的距离为半径画圆即可；
（2）作BH⊥OA，垂足为H首先根据sin∠BOA及BO=10计算出B点坐标，然后根据勾股定理求出AB长，可得cos∠BAO；
（3）分三种情况进行计算，①当BO=AB时，②当AO=AB′时，③当AO=OB″时，，因为点B是沿x轴正半轴方向平移，因此B点纵坐标不变，依次利用勾股定理求出其横坐标即可。