题目内容
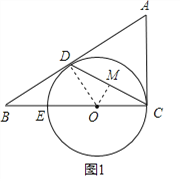
【题目】如图,△ABC中,∠ACB=90°,D是边AB上一点,且∠A=2∠DCB.E是BC边上的一点,以EC为直径的⊙O经过点D.
(1)求证:AB是⊙O的切线;
(2)若CD的弦心距为1,BE=EO,求BD的长.

【答案】(1)证明见解析;(2)BD=2![]() .
.
【解析】试题分析:(1)连接OD,如图1所示,由OD=OC,根据等边对等角得到一对角相等,再由∠DOB为△COD的外角,利用三角形的外角等于与它不相邻的两个内角之和,等量代换可得出∠DOB=2∠DCB,又∠A=2∠DCB,可得出∠A=∠DOB,又∠ACB=90°,可得出直角三角形ABC中两锐角互余,等量代换可得出∠B与∠ODB互余,即OD垂直于BD,确定出AB为圆O的切线,得证;
(2)法1:过O作OM垂直于CD,根据垂径定理得到M为DC的中点,由BD垂直于OD,得到三角形BDO为直角三角形,再由BE=OE=OD,得到OD等于OB的一半,可得出∠B=30°,进而确定出∠DOB=60°,又OD=OC,利用等边对等角得到一对角相等,再由∠DOB为三角形DOC的外角,利用外角的性质及等量代换可得出∠DCB=30°,在三角形CMO中,根据30°角所对的直角边等于斜边的一半得到OC=2OM,由弦心距OM的长求出OC的长,进而确定出OD及OB的长,利用勾股定理即可求出BD的长;
法2:过O作OM垂直于CD,连接ED,由垂径定理得到M为CD的中点,又O为EC的中点,得到OM为三角形EDC的中位线,利用三角形中位线定理得到OM等于ED的一半,由弦心距OM的长求出ED的长,再由BE=OE,得到ED为直角三角形DBO斜边上的中线,利用直角三角形斜边上的中线等于斜边的一半,由DE的长求出OB的长,再由OD及OB的长,利用勾股定理即可求出BD的长.
试题解析:(1)证明:连接OD,如图1所示:
∵OD=OC,
∴∠DCB=∠ODC,
又∠DOB为△COD的外角,
∴∠DOB=∠DCB+∠ODC=2∠DCB,
又∵∠A=2∠DCB,
∴∠A=∠DOB,
∵∠ACB=90°,
∴∠A+∠B=90°,
∴∠DOB+∠B=90°,
∴∠BDO=90°,
∴OD⊥AB,
又∵D在⊙O上,
∴AB是⊙O的切线;
(2)解法一:
过点O作OM⊥CD于点M,如图1,
∵OD=OE=BE=![]() BO,∠BDO=90°,
BO,∠BDO=90°,
∴∠B=30°,
∴∠DOB=60°,
∵OD=OC,
∴∠DCB=∠ODC,
又∵∠DOB为△ODC的外角,
∴∠DOB=∠DCB+∠ODC=2∠DCB,
∴∠DCB=30°,
∵在Rt△OCM中,∠DCB=30°,OM=1,
∴OC=2OM=2,
∴OD=2,BO=BE+OE=2OE=4,
∴在Rt△BDO中,根据勾股定理得:BD=![]() ;
;
解法二:
过点O作OM⊥CD于点M,连接DE,如图2,
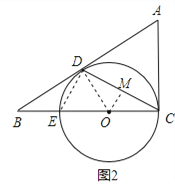
∵OM⊥CD,
∴CM=DM,又O为EC的中点,
∴OM为△DCE的中位线,且OM=1,
∴DE=2OM=2,
∵在Rt△OCM中,∠DCB=30°,OM=1,
∴OC=2OM=2,
∵Rt△BDO中,OE=BE,
∴DE=![]() BO,
BO,
∴BO=BE+OE=2OE=4,
∴OD=OE=2,
在Rt△BDO中,根据勾股定理得BD=![]() .
.
考点: 1.切线的判定;2.含30度角的直角三角形;3.垂径定理;4圆周角定理.