题目内容
【题目】如图,O是直线AB上的一点,∠COD是直角,OE平分∠BOC.

(1)若∠AOC=30°,求∠DOE的度数;
(2)若∠AOC=α,直接写出∠DOE的度数(用含α的代数式表示);
(3)在(1)的条件下,∠BOC的内部有一射线OG,射线OG将∠BOC分为1:4两部分,求∠DOG的度数.
【答案】(1)15°(2)![]() α(3)①60°②30°
α(3)①60°②30°
【解析】
(1)由已知可求出∠BOD=180°-90°-30°=60°,再由∠COB是150°,OE平分∠BOC求出∠DOE的度数;(2)根据(1)的解题思路,可求出∠DOE的度数;(3) ∠BOC的内部有有一射线OG,射线OG将∠BOC分为1:4两部分,题中没有明确射线OG的位置,分情况解答即可.
(1)∵∠COD是直角,∠AOC=30°,
∴∠BOD=180°﹣90°﹣30°=60°,
∴∠COB=90°+60°=150°,
∵OE平分∠BOC,
∴∠BOE=![]() ∠BOC=75°,
∠BOC=75°,
∴∠DOE=∠BOE﹣∠BOD=75°﹣60°=15°.
(2)∵∠COD是直角,∠AOC=α,
∴∠BOD=180°﹣90°﹣α=90°﹣α,
∴∠COB=90°+90°﹣α=180°﹣α,
∵OE平分∠BOC,
∴∠BOE=![]() ∠BOC=90°﹣
∠BOC=90°﹣![]() α,
α,
∴∠DOE=∠BOE﹣∠BOD=90°﹣![]() α﹣(90°﹣α)=
α﹣(90°﹣α)=![]() α.
α.
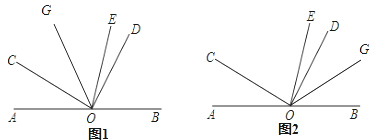
(3)①当射线OG位于DC之间时,如图1所示
∵∠AOC=30°,射线OG将∠BOC分为1:4两部分,
∴∠BOC=150°,∠COG=30°,∠BOG=120°
由(1)知:∠BOD=60°,
∴∠DOG=∠BOG﹣∠BOD=120°﹣60°=60°
②当射线OG位于DB之间时,如图2所示
∵∠AOC=30°,射线OG将∠BOC分为1:4两部分,
∴∠BOC=150°,∠COG=120°,∠BOG=30°
由(1)知:∠BOD=60°,
∴∠DOG=∠BOD﹣∠BOG=60°﹣30°=30°