题目内容
【题目】如图,已知∠AOB,点P是∠AOB内部的一个定点,点E、F分别是OA、OB上的动点.
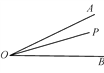
(1)要使得△PEF的周长最小,试在图上确定点E、F的位置.
(2)若OP=4,要使得△PEF的周长的最小值为4,则∠AOB=________.
【答案】(1) 作图见解析. (2)30°
【解析】试题分析:
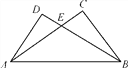
(1)分别作点P关于OA的对称点C,关于OB的对称点D,连接CD,交OA于E,OB于F.
(2)由轴对称的性质知OP=OC,OP=OD,且△PEF周长的最小值是CD,所以dqga4OCD是等边三角形,而∠COD=2∠EOF,由此即可求解.
试题解析:
(1)如图,作点P关于OA的对称点C,关于OB的对称点D,连接CD,交OA于E,OB于F.此时,△PEF的周长最小.
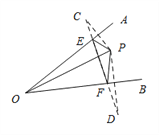
(2)根据轴对称的性质得,OC=OP=OD,∠COE=∠POE,∠DOF=∠POF,△PEF的周长的最小值=CD,
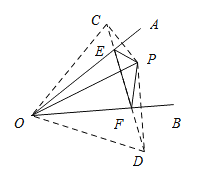
因为OP=4,△PEF的周长的最小值为4,所以△OCD是等边三角形.
因为∠COE=∠POE,∠DOF=∠POF,所以∠PEF=![]() ∠COD=30°.
∠COD=30°.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目