题目内容
【题目】在四边形ABCD中,AB=CD,M、N分别是AD和BC的中点,延长BA和CD分别交射线NM于点E和点F,若tan∠F=![]() , FC=FN,EN=
, FC=FN,EN=![]() , 则EF=
, 则EF= 
【答案】1
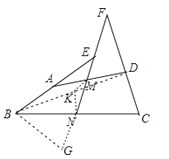
【解析】解:连接BD,点K为BD的中点;连接KM、KN;延长MN至G点,使EG=EB,连接BG.
∵M、N分别是AD和BC的中点,
∴KM∥AB,AB=2KM、KN∥CD,CD=2KN.
∵AB=CD,
∴KM=KN,
∴△KMN为等腰三角形,
∴∠KMN=∠KNM,
∵KM∥AB
∴∠BEG=∠KMN,
∵KN∥CD,
∴∠F=∠KNM
∴∠F=∠KNM=∠KMN=∠BEG,
∵FC=FN、EB=EG,
∴△EBG和△FCN均为等腰三角形,且△EBG∽△FCN.
∴∠G=∠C=∠FNC,
又∵∠BNG=∠FNC,
∴∠G=∠BNG,
∴△BGN为等腰三角形,
∴BN=BG,∠EBG=∠G,
∴BG=CN,∠EBG=∠FNC,
在△EBG和△FNC中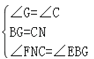 ,
,
∴△EBG≌△FCN(ASA),
∴EG=FN,
∴EF=NG,
过B点作GN的垂线BH交GN于H点.
由△BGN为等腰△可知,HN=HG,
∵tan∠F=![]() ,
,
∴设BH=3a.
∴tan∠BEG=tan∠F=![]() ,
,
∴EH=4a、BE=5a,
∴HG=HN=BE﹣EH=a,
∵EN=HE﹣HN=4a﹣a=3a,
∵EN=![]() , 所以3a=
, 所以3a=![]() ,
,
∴a=![]() , EF=NG=2a=1,
, EF=NG=2a=1,
所以答案是:1.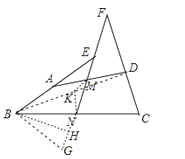
【考点精析】本题主要考查了三角形中位线定理的相关知识点,需要掌握连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半才能正确解答此题.

 小学教材全测系列答案
小学教材全测系列答案【题目】我市某绿色无公害蔬菜基地有甲、乙两种植户,他们们种植了A、B两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如下表:
种植户 | 种植A类蔬菜面积(单位:亩) | 种植B类蔬菜面积(单位:亩) | 总收入(单位:元) |
甲 | 1 | 3 | 13500 |
乙 | 2 | 2 | 13000 |
说明:不同种植户种植的同类蔬菜每亩平均收入相等
(1)求A、B两类蔬菜每亩平均收入各是多少元?
(2)今年甲、乙两种植户联合种植,计划合租50亩地用来种植A、B两类蔬菜,为了使总收入不低于16400元,问联合种植最多可以种植A类蔬菜多少亩?







