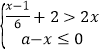题目内容
【题目】在平面直角坐标系xOy中,抛物线y=x2+bx+c经过点A(﹣1,t),B(3,t),与y轴交于点C(0,﹣1).一次函数y=x+n的图象经过抛物线的顶点D.
(1)求抛物线的表达式;
(2)求一次函数y=x+n的表达式;
(3)将直线l:y=mx+n绕其与y轴的交点E旋转,使当﹣1≤x≤1时,直线l总位于抛物线的下方,请结合函数图象,求m的取值范围.
【答案】解:(1)二次函数的对称轴是x=![]() =1,
=1,
则﹣![]() =1,
=1,
解得:b=﹣2,
∵抛物线与y轴交于点C(0,﹣1).
∴c=﹣1,
则二次函数的解析式是y=x2﹣2x﹣1;
(2)二次函数y=x2﹣2x﹣1的顶点坐标是(1,﹣2),
代入y=x+n得﹣2=1+n,
解得:n=﹣3,
则一次函数y=x+n的表达式是y=x﹣3;
(3)如图所示: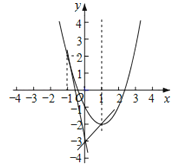
在y=x2﹣2x﹣1中,当x=﹣1时,y=2;
当x=1时,y=﹣2.
当直线y=mx﹣3经过点(﹣1,2)时,﹣m﹣3=2,解得:m=﹣5;
当直线y=mx﹣3经过点(1,﹣2)时,m﹣3=﹣2,解得:m=1.
则当﹣5<m<1时,当﹣1≤x≤1时,直线l总位于抛物线的下方.
【解析】(1)根据A和B对称,可求得对称轴,则b的值即可求得,然后根据函数经过点(0,﹣1),代入即可求得c的值,则抛物线解析式即可求得;
(2)首先求得抛物线的顶点,代入一次函数解析式即可求得n的值,求得一次函数的解析式;
(3)首先求得抛物线上当x=﹣1和x=1时对应点的坐标,然后求得直线y=mx+n经过这两个点时对应的m的值,据此即可求解.
【考点精析】通过灵活运用确定一次函数的表达式,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法即可以解答此题.

练习册系列答案
相关题目