题目内容
【题目】如图,在直角梯形ABCD中,AB∥CD,AD⊥DC,AB=BC,且AE⊥BC.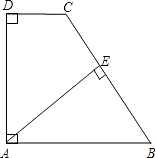
(1)求证:AD=AE;
(2)若AD=8,DC=4,求AB的长.
【答案】
(1)证明:连接AC,
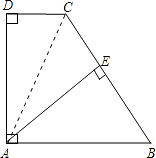
∵AB∥CD,
∴∠ACD=∠BAC,
∵AB=BC,
∴∠ACB=∠BAC,
∴∠ACD=∠ACB,
∵AD⊥DC,AE⊥BC,
∴∠D=∠AEC=90°,
∵AC=AC,
∴ 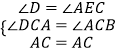 ,
,
∴△ADC≌△AEC,(AAS)
∴AD=AE
(2)解:由(1)知:AD=AE,DC=EC,
设AB=x,则BE=x﹣4,AE=8,
在Rt△ABE中∠AEB=90°,
由勾股定理得:82+(x﹣4)2=x2,
解得:x=10,
∴AB=10.
说明:依据此评分标准,其它方法如:过点C作CF⊥AB用来证明和计算均可得分.
【解析】(1)连接AC证明AD、AE所在的三角形全等,即证明△ADC≌△AEC,即可得出结论。
(2)设AB=x,再用含x的代数式表示BE,利用勾股定理得到关于x的方程,求解即可。
【考点精析】本题主要考查了勾股定理的概念和直角梯形的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;一腰垂直于底的梯形是直角梯形才能正确解答此题.

练习册系列答案
相关题目
【题目】在下图的直角坐标系中,将△ABC平移后得到△A’B’C’,它们的个顶点坐标如下表所示
△ABC | A(0,0) | B(3,0) | C(5,5) |
△A'B'C' | A'(4,2) | B'(7,b) | C'(c,d) |
(1)观察表中各对应点坐标的变化,并填空:△ABC向______平移______个单位长度,再向______平移______个单位长度可以得到△A'B'C';
(2)在坐标系中画出△ABC及平移后的△A'B'C';
(3)求出△A'B'C'的面积.