题目内容
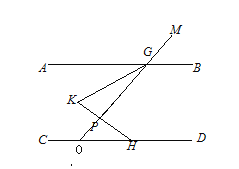
【题目】如图,AB//CD,点G在直线AB上, 点H在直线CD上,点K在AB、CD之间且在G、H所在直线的左侧, 若 ∠GKH=60°,点P为线段KH上一点(不和K、H重合),连接PG并延长到M, 设∠KHC=n∠KGP,要使得![]() 为定值,则n=_____
为定值,则n=_____

【答案】3
【解析】
延长MP交CD于点O,设∠KGP=x,则∠KHC=nx,利用平行线的性质以及三角形外角性质,即可得到∠GPH=60°+x,∠AGM=∠COM=120°+(n-1)x,由![]() 为定值可得n的值.
为定值可得n的值.
解:延长MP交CD于点O,
设∠KGP=x,则∠KHC=nx,
∵∠GKH=60°,
∴∠GPH=60°+x,
∠OPH=180°-(60°+x)=120°-x,
∵AB∥CD,
∴∠AGM=∠COM=∠OPH+∠KHC=120°-x+ nx=120°+(n-1)x,
∴![]() =
=![]()
∵n-1=2时,![]() 为定值:
为定值:![]() =
=![]() =2,
=2,
∴n-1=2,n=3.
故答案为:3.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目