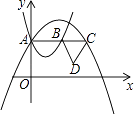题目内容
【题目】如图,在平面直角坐标系中,直线l所对应的函数表达式为y=x.过点A1(0,1)作y轴的垂线交直线l于点B1 , 过点B1作直线l的垂线交y轴于点A2;过点A2作y轴的垂线交直线l于点B2 , 则点B2的坐标为( )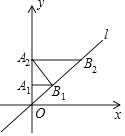
A.(1,1)
B.( ![]() ,
, ![]() )
)
C.(2,2)
D.( ![]() ,
, ![]() )
)
【答案】C
【解析】解:∵直线l所对应的函数表达式为y=x,
∴l与x轴正半轴的夹角为45°,
∵A1B1∥x轴,
∴∠A1B1O=∠A1OB1=45°,
∵A1(0,1),OA1=1,
∴A1B1=1,
∴B1(1,1).
∵A2B1⊥l,
∴∠OA2B1=∠A1B1A2=45°,
∴OA2=2,
∴A2(0,2),
∵A2B2∥x轴,
∴∠A2B2O=∠A2OB2=45°,
∴A2B2=OA2=2,
∴B2(2,2).
所以答案是:C.
【考点精析】本题主要考查了等腰直角三角形和垂线的性质的相关知识点,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短才能正确解答此题.

练习册系列答案
相关题目