题目内容
【题目】已知二次函数y=ax2+bx﹣3经过A(﹣1,0),B(3,0)两点,
(1)求二次函数解析式及对称轴方程;
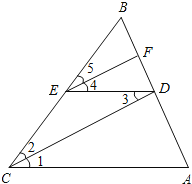
(2)连接BC,交对称轴于点E,求E点坐标;
(3)在y轴上是否存在一点M,使△BCM为等腰三角形?若存在,直接写出点M的坐标;若不存在,请说明理由;
(4)在第四象限内抛物线上是否存一点H,使得四边形ACHB的面积最大?若存在,求出点H坐标;若不存在,说明理由.
【答案】
(1)解:将A,B两点坐标代入y=ax2+bx﹣3得:
![]() ,解得a=1,b=﹣2,
,解得a=1,b=﹣2,
所以二次函数解析式为y=x2﹣2x﹣3,
对称轴方程为:直线x=﹣ ![]() =1
=1
(2)解:如图1,y=x2﹣2x﹣3,
∴C(0,﹣3),
设直线BC的解析式为:y=kx+b(k≠0),
把B(3,0)和C(0,﹣3)代入得: ![]() ,
,
解得: ![]() ,
,
∴直线BC的解析式为:y=x﹣3,
当x=1时,y=1﹣3=﹣2,
∴E(1,﹣2)
(3)解:存在:
如图2,有四种情况:
①当BC=BM1时,
∵x轴⊥y轴,
∴OM1=OC=3,
∴M1(0,3),
②当BC=CM2时(M2在点C的上方),
∵BC= ![]() =3
=3 ![]() ,
,
∴CM2=3 ![]() ,
,
∴OM2=3 ![]() ﹣3,
﹣3,
∴M2(0,3 ![]() ﹣3),
﹣3),
③当BC=CM3时(M3在C的下方),
∴OM3=3 ![]() +3,
+3,
∴M3(0,﹣3﹣3 ![]() ),
),
④作BC的中垂线,交BC于E,交y轴于M4,

cos∠M4CB= ![]() ,
,
∴ ![]() ,
,
CM4=3,即M4与原点O重合,
∴M4(0,0),
综上所述,点M的坐标为:M1(0,3),M2(0,3 ![]() ﹣3),M3(0,﹣3﹣
﹣3),M3(0,﹣3﹣ ![]() ),M4(0,0)
),M4(0,0)
(4)解:如图3,连接OH,设H点坐标为(x,x2﹣2x﹣3),

S四边形ACHB=S△AOC+S△COH+S△BOH,
= ![]() +
+ ![]() x+
x+ ![]() |x2﹣2x﹣3|,
|x2﹣2x﹣3|,
= ![]() +
+ ![]() x+
x+ ![]() (﹣x2+2x+3),
(﹣x2+2x+3),
=﹣ ![]() +
+ ![]() x+6,
x+6,
=﹣ ![]() (x﹣
(x﹣ ![]() )2+
)2+ ![]() ,
,
∴当x= ![]() 时,四边形ACHB的面积最大,
时,四边形ACHB的面积最大,
∴当x0= ![]() 时,x02﹣2x0﹣3=
时,x02﹣2x0﹣3= ![]() ,
,
所以点H坐标为 ![]() .
.
【解析】(1)利用待定系数法求解析式,利用对称轴公式求对称轴方程;
(2)利用求BC解析式求点E的坐标为(1,-2);
(3)分别以△BCM的三边为腰画等腰三角形,与y轴有四个交点,分别求出M点的坐标即可;
(4)设H点坐标为(x,x2-2x-3),因为H在第四象限,可以取H的纵坐标的相反数为△OBH的高,利用面积和表示四边形ACHB的面积,利用二次函数的最值得结论.
【考点精析】本题主要考查了确定一次函数的表达式和二次函数的最值的相关知识点,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a才能正确解答此题.

【题目】某书店为了迎接“读书节”制定了活动计划,以下是活动计划书的部分信息:
“读书节”活动计划书 | ||
书本类别 | A类 | B类 |
进价(单位:元) | 18 | 12 |
备注 | 1、用不超过16800元购进A、B两类图书共1000本; | |
(1)陈经理查看计划数时发现:A类图书的标价是B类图书标价的1.5倍,若顾客用540元购买的图书,能单独购买A类图书的数量恰好比单独购买B类图书的数量少10本,请求出A、B两类图书的标价;
(2)经市场调查后,陈经理发现他们高估了“读书节”对图书销售的影响,便调整了销售方案,A类图书每本标价降低a元(0<a<5)销售,B类图书价格不变,那么书店应如何进货才能获得最大利润?
【题目】八(3)班在一次班会课上,就“遇见路人摔倒后如何处理”的主题进行讨论,并对全班50名学生的处理方式进行统计,得出相关统计表和统计图(如图)
组别 | A | B | C | D |
处理方式 | 迅速离开 | 马上救助 | 视情况而定 | 只看热闹 |
人数 | m | 30 | n | 5 |
请根据表图所提供的信息回答下列问题:
(1)统计表中的m= ,n= ;
(2)补全频数分布直方图;
(3)若该校有3000名学生,请据此估计该校学生采取“马上救助”方式的学生有多少人?