题目内容
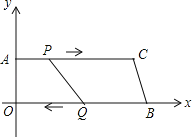
【题目】如图,已知A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,点Q以2cm/s的速度向点D移动,当点P运动到点B停止时,点Q也随之停止运动,问:
(1)P、Q两点从开始出发多长时间时,四边形PBCQ的面积是33![]() ?
?
(2)P、Q两点从开始出发多长时间时,点P与Q之间的距离是10cm?

【答案】(1) 5秒;(2) 4.8秒或1.6秒.
【解析】
(1)根据矩形和正方形的性质,利用梯形面积的求算方法,找出等量关系列出方程求解即可;
(2)作PE⊥CD,垂足为E,设运动时间为t秒,用t表示线段长,用勾股定理列方程求解.
(1)依题意得
AP=3t,
BP=AB-AP=16-3t,
CQ=2t,
DQ=DC-CQ=16-2t,
故S梯形PBCQ﹦![]() ﹙CQ+PB﹚BC.
﹙CQ+PB﹚BC.
又∵S梯形PBCQ﹦33,
∴![]() ﹙2t+16-3t﹚×6=33,
﹙2t+16-3t﹚×6=33,
解得t=5.
答:P、Q两点出发后5秒时,四边形PBCQ的面积为33cm2.
(2)过点P做PE⊥CD交CD于E.

QE=DQ-AP=16-5t,
在Rt△PQE中,
PE2+QE2=PQ2,
可得:(16-5t)2+62=102,
解得t1=4.8,t2=1.6.
故P、Q两点从开始出发4.8秒或1.6秒时,点P与Q之间的距离是10cm.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目