题目内容
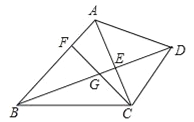
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,D为△ABC内一点, ∠BAD=15°,AD=AC,CE⊥AD于E,且CE=5.
(1)求BC的长;
(2)求证:BD=CD.

【答案】(1)、10;(2)、证明过程见解析
【解析】
试题分析:(1)、根据等腰直角三角形的性质得出∠BAC=45°,从而得出∠CAD=30°,根据垂直得出AC=BC=10;(2)、过D作DF⊥BC于F,然后证明Rt△DCE和Rt△DCF全等,从而得出CF=CE=5,根据BC=10得出BF=FC,从而得出答案.
试题解析:(1)、在△ABC中, ∵AC=BC,∠ACB=90°,∴∠BAC=45°.
∵∠BAD=15°,∴∠CAD=30°. ∵CE⊥AD,CE=5,∴AC=10.∴BC=10.
(2)、过D作DF⊥BC于F.在△ADC中,∠CAD=30°,AD=AC,∴∠ACD=75°.
∵∠ACB=90°,∴∠FCD=15°. 在△ACE中,∠CAE=30°,CE⊥AD,∴∠ACE=60°.
∴∠ECD=∠ACD-∠ACE=15°.∴∠ECD=∠FCD.∴DF=DE.
在Rt△DCE与Rt△DCF中,![]() ∴Rt△DCE≌Rt△DCF.
∴Rt△DCE≌Rt△DCF.
∴CF=CE=5.∵BC=10,∴BF=FC. ∵DF⊥BC,∴BD=CD.

练习册系列答案
相关题目