题目内容
【题目】如图,在直角坐标系中,抛物线y=﹣(x+1)2+4与x轴交于点A、B,与y轴交于点C.
(1)写出抛物线顶点D的坐标 ;
(2)点D1是点D关于y轴的对称点,判断点D1是否在直线AC上,并说明理由;
(3)若点E是抛物线上的点,且在直线AC的上方,过点E作EF⊥x轴交线段AC于点F,求线段EF的最大值.
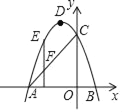
【答案】(1) (﹣1,4);(2)见解析;(3) 2.25.
【解析】
(1)根据二次函数的解析式直接写出即可;
(2)先根据二次函数求出A、C的坐标,再用待定系数法确定直线AC的关系式,再求出
点D1,把它代入直线判断是否再直线上;
(3)设点E(x,﹣x2﹣2x+3),F(x,x+3),则EF=(﹣x2﹣2x+3)﹣(x+3)=﹣x2﹣3x=﹣(x+1.5)2+2.25, 则可知x=-1.5时,EF的最大值2.25.
解:(1)∵y=﹣(x+1)2+4,
∴抛物线顶点D的坐标是(﹣1,4).
故答案为(﹣1,4);
(2)点D1在直线AC上,理由如下:
∵抛物线y=﹣(x+1)2+4与x轴交于点A、B,与y轴交于点C,
∴当y=0时,﹣(x+1)2+4=0,解得x=1或﹣3,A(﹣3,0),B(1,0),
当x=0时,y=﹣1+4=3,C(0,3).
设直线AC的解析式为y=kx+b,
由题意得![]() ,解得
,解得![]() ,
,
∴直线AC的解析式为y=x+3.
∵点D1是点D关于y轴的对称点,D(﹣1,4).
∴D1(1,4),
∵x=1时,y=1+3=4,
∴点D1在直线AC上;
(3)设点E(x,﹣x2﹣2x+3),则F(x,x+3),
∵EF=(﹣x2﹣2x+3)﹣(x+3)=﹣x2﹣3x=﹣(x+1.5)2+2.25,
∴线段EF的最大值是2.25.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目