题目内容
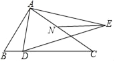
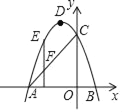
【题目】已知在△ABC中,AB=AC,AD⊥BC,垂足为点D,以AD为对角线作正方形AEDF,DE交AB于点M,DF交AC于点N,连结EF,EF分别交AB、AD、AC于点G、点O、点H.
(1)求证:EG=HF;
(2)当∠BAC=60°时,求![]() 的值;
的值;
(3)设![]() ,△AEH和四边形EDNH的面积分别为S1和S2,求
,△AEH和四边形EDNH的面积分别为S1和S2,求![]() 的最大值.
的最大值.

【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据等腰三角形的判定与性质,正方形的性质易证△AGH为等腰三角形,通过“三线合一”可得OG=OH,即可得证;
(2)由等边三角形的性质可设OH=a,则OA=OE=OF=![]() a,则EH=(
a,则EH=(![]() )a,HF=(
)a,HF=(![]() )a,
)a,
根据相似三角形判定易证△AEH∽△NFH,△AOH∽△ADC,△HNF∽△CND,然后通过相似三角形的对应边成比整理即可得解;
(3)设EH=2m,则FH=2km,OA=![]() EF=(k+1)m,分别得到S1、S△HNF和S△EDF关于k,m的表达式,再根据S2=S△EDF - S△HNF得到S2的表达式,进而得到
EF=(k+1)m,分别得到S1、S△HNF和S△EDF关于k,m的表达式,再根据S2=S△EDF - S△HNF得到S2的表达式,进而得到![]() 关于k的表达式,通过配方法即可得解.
关于k的表达式,通过配方法即可得解.
(1)在正方形AEDF中,OE=OF,EF⊥AD,
∵AD⊥BC,
∴EF∥BC,
∴∠AGH=∠B,∠AHG=∠C,
而AB=AC,
∴∠B=∠C,
∴∠AGH=∠AHG,
∴AG=AH,
∴OG=OH,
∴OE-OG=OF-OH,
∴EG=FH;
(2)当∠BAC=60°时,△ABC为正三角形,
∵AD⊥EF,
∴∠OAH=30°,
∴![]() ,
,
设OH=a,则OA=OE=OF=![]() a,
a,
∴EH=(![]() )a,HF=(
)a,HF=(![]() )a,
)a,
∵AE∥FN,
∴△AEH∽△NFH,
∴![]() ,
,
∵EF∥BC,
∴△AOH∽△ADC,
∴![]() ,
,
∴CD=2a,
易证△HNF∽△CND,
∴![]() ,
,
∴![]() ;
;
(3)设EH=2m,则FH=2km,OA=![]() EF=(k+1)m,
EF=(k+1)m,
∴S1=(k+1)m2,
由(2)得,△AEH∽△NFH,
∴S△HNF=k2S1=k2(k+1)m2,
∴S2=S△EDF - S△HNF =(k+1)2m2 -k2(k+1)m2=(-k2+k+1)(k+1)m2,
∴![]() =-k2+k+1,
=-k2+k+1,
∴当k=![]() 时,
时,![]() 最大=
最大=![]() .
.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案