Question

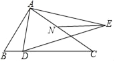
【题目】如图，△ABC与△ADE都是等腰直角三角形，连接CD、BE，CD、BE相交于点O，△BAE可看作是由△CAD顺时针旋转所得．

（1）旋转中心是 ，旋转角度是 ；

（2）判断CD与BE的位置关系，并说明理由．

Answer 1

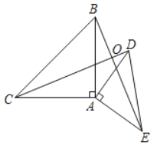
【答案】（1）点A，90°；（2）CD⊥BE，理由见解析.

【解析】

（1）由图形可得旋转中心为点A，旋转角为∠CAB为90°；

（2）由旋转得△ACD≌△ABE，再利用全等三角形的性质与角的等量替换即可求得∠BOC＝90°，即得证.

解：（1）由图形可得旋转中心为点A，旋转角为∠CAB，即旋转角度为90°，

故答案为：点A，90°

（2）CD⊥BE

理由如下：∵△BAE可看作是由△CAD顺时针旋转所得，

∴△ACD≌△ABE

∴∠ACD＝∠ABE，

∵在Rt△ABC中，∠ACD+∠BCD+∠ABC＝90°，

∴∠BCD+∠ABC+∠ABE＝90°

∴∠BOC＝90°

∴CD⊥BE