题目内容
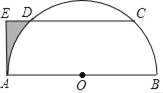
【题目】如图,AB是半圆O的直径,C,D是半圆O上的两点,弧AC=弧BD,AE与弦CD的延长线垂直,垂足为E.
(1)求证:AE与半圆O相切;
(2)若DE=2,AE=![]() ,求图中阴影部分的面积
,求图中阴影部分的面积
【答案】(1)详见解析;(2)![]() .
.
【解析】
![]() 从问题入手,根据切线的判定可知,要证明AE与半圆O相切,必须证明AE⊥AB, 由已知条件:AE与弦CD的延长线垂直,进而须证明
从问题入手,根据切线的判定可知,要证明AE与半圆O相切,必须证明AE⊥AB, 由已知条件:AE与弦CD的延长线垂直,进而须证明![]() ,联想证平行的办法与弧建立联系;
,联想证平行的办法与弧建立联系;
![]() 作辅助线,构建直角三角形,先由勾股定理可得:
作辅助线,构建直角三角形,先由勾股定理可得:![]() ,由直角三角形斜边中线的性质求得:ED=EF=DF=2, 则△DEF是等边三角形,再求得△AOD是等边三角形,根据面积差可得阴影部分的面积.
,由直角三角形斜边中线的性质求得:ED=EF=DF=2, 则△DEF是等边三角形,再求得△AOD是等边三角形,根据面积差可得阴影部分的面积.
(1)证明:连接AC,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(2)解:连接AD,取AD的中点F,连接EF、OD,
![]()
![]()
∵F是AD的中点,
![]()
∴ED=EF=DF=2,
∴△DEF是等边三角形,
∴∠EDA=60°,
由(1)知:AB∥CF
∴∠DAO=∠EDA=60°,
∵OA=OD,
∴△AOD是等边三角形,
∴∠AOD=60°,OA=AD=4,
![]()

练习册系列答案
相关题目