题目内容
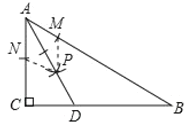
【题目】如图,在Rt△ABC 中,∠C=90°,∠B=30°,以点 A 为圆心,任意长为半径画弧分别交 AB,AC 于点M 和 N,再分别以 M,N 为圆心,大于![]() 的长为半径画弧,两弧交于点 P,连接 AP 并延长交 BC 于点D,则下列说法中:①AD 是∠BAC 的平分线;②点 D 在线段 AB 的垂直平分线上;③S△DAC:S△ABC=1:2.正确的是( ).
的长为半径画弧,两弧交于点 P,连接 AP 并延长交 BC 于点D,则下列说法中:①AD 是∠BAC 的平分线;②点 D 在线段 AB 的垂直平分线上;③S△DAC:S△ABC=1:2.正确的是( ).
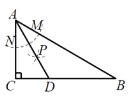
A.①②B.①③C.②③D.①②③
【答案】A
【解析】
①连接NP,MP,根据SSS定理即可得证![]() ,从而得出结论.②先根据三角形内角和定理得∠CAB的度数,再由AD 是∠BAC 的平分线得出
,从而得出结论.②先根据三角形内角和定理得∠CAB的度数,再由AD 是∠BAC 的平分线得出![]() ,根据
,根据![]() 可知
可知![]() ,故可得出结论.③先根据直角三角形的性质得出
,故可得出结论.③先根据直角三角形的性质得出![]() ,
,![]() ,再由三角形的面积公式即可得出结论.
,再由三角形的面积公式即可得出结论.
①连接NP,MP
在△ANP和△AMP中
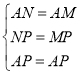
∴![]()
∴![]()
故AD 是∠BAC 的平分线,①正确
②∵在△ABC中,![]() ,
,![]()
∴![]()
∵AD 是∠BAC 的平分线
∴![]()
∴![]()
∴![]()
∴点 D 在线段 AB 的垂直平分线上,故②正确
③∵在Rt△ACD中,![]()
∴![]()
∴![]() ,
,![]()
∴![]()
∴![]() ,故③错误
,故③错误
故正确的有①②
故答案为:A.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目