Question

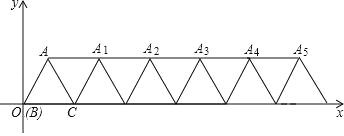
【题目】如图，在平面直角坐标系内，边长为 4 的等边△ABC 的顶点 B 与原点重合，将△ABC 绕顶点 C 顺时针旋转 60°得到△ACA1，将四边形 ABCA1看作一个基本图形，将此基本图形不断复制并平移，请回答：

（1）求点 A的坐标；点 A1的坐标．

（2）求A2018的坐标．

Answer 1

【答案】（1）（2，2）；（6，2）；（2）（8074，2）．

【解析】

因为边长为 4 的等边△ABC 的顶点 B 与原点重合，所以OA=BC=4，∠AOC=60°，过点 A 作 AD⊥x 轴于点 D，所以，即可求得A点坐标，再因为四边形 是平行四边形， =BC=4，∥BC，即可求得点坐标.

将四边形ABCA1 看作一个基本图形，将此基本图形不断复制并平移，根据规律可得

，代入即可求得答案.

（1）∵边长为 4 的等边△ABC 的顶点 B 与原点重合，

∴OA=BC=4，∠AOC=60°．

如图，过点 A 作 AD⊥x 轴于点 D，

∴BD=DC= BC=2，AD=2

∴点 A 的坐标为（2，2）．

∵将△ABC 绕顶点 C 顺时针旋转 60°得到△ACA1，

∴四边形 ABCA1 是平行四边形，

∴AA1=BC=4，AA1∥BC，

∴点 A1 的坐标为（2+4，2），即（6，2）．故答（2，2）；（6，2）．

（2）∵将四边形ABCA1 看作一个基本图形，将此基本图形不断复制并平移，

∴点 A2 的坐标为（2+4×2，2），即（10，2）；点 A3 的坐标为（2+4×3，2），即（14，2）；……；

∴点 A2018 的坐标为（2+4×2018，2），

即（8074，2）．