Question

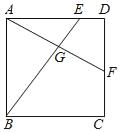
【题目】如图，△ABC是⊙O的内接三角形，∠BAC的角平分线AE交⊙O于点E，交BC于点D，过点E作直线l∥BC．

（1）判断直线l与⊙O的位置关系，并说明理由；

（2）若在AE上取一点F使EF=BE，求证：BF是∠ABC的平分线；

（3）在（2）的条件下，若DE=3，BE=5，求AE的长．

Answer 1

【答案】（1）直线l与⊙O相切，见解析；（2）见解析；（3）AE=．

【解析】

（1）连接OE，由AE平分∠BAC知=，据此得OE⊥BC，根据l∥BC可得OE⊥l，从而得证；

（2）由BE=EF知∠EBF=∠EFB，由∠EFB=∠BAE+∠ABF、∠EBF=∠CBE+∠CBF及∠CBE=∠CAE=∠BAE可得∠ABF=∠CBF，从而得证；

（3）证△BED∽△AEB得=，据此可得答案．

（1）直线l与⊙O相切，

如图1，连接OE，

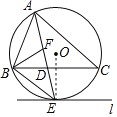
∵AE平分∠BAC，

∴∠BAE=∠CAE，

∴=，

∴半径OE⊥BC，

∵l∥BC，

∴OE⊥l，

∴直线l与⊙O相切；

（2）∵BE=EF，

∴∠EBF=∠EFB，

∵∠EFB=∠BAE+∠ABF，∠EBF=∠CBE+∠CBF，

∴∠CBE+∠CBF=∠BAE+∠ABF，

∵∠CBE=∠CAE=∠BAE，

∴∠ABF=∠CBF，

∴BF平分∠ABC；

（3）∵∠DBE=∠BAE，∠DEB=∠BEA，

∴△BED∽△AEB，

∴=，即=，

解得：AE=．