题目内容
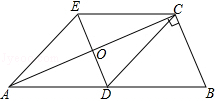
【题目】已知:如图,在平行四边形ABCD和矩形ABEF中,AC与DF相交于点G.
(1) 试说明DF=CE;
(2) 若AC=BF=DF,求∠ACE的度数.
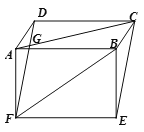
【答案】(1)证明见解析;(2)∠ACE=60°
【解析】(1)证明四边形ABDF是平行四边形,再利用平行四边形一组对边平行且相等可证出结论;(2)由矩形的性质得首先证明BF=AE,再证AC=AE=CE即可得出结论.
解:(1)∵四边形ABCD是平行四边形,∴AB=DC,AB//DC
又∵四边形ABEF是矩形,∴AB=EF,AB//EF
∴DC=EF,DC//EF.
∴四边形DCEF是平行四边形.
∴DF=CE.
(2)连结AE,∵四边形ABEF是矩形∴BF=AE
又∵AC=BF=DF ∴AC=AE=CE
∴△ AEC是等边三角形,∴∠ACE=60°.
“点睛”本题考查了平行四边形的性质和判定以及矩形的性质,等边三角形的性质,解题关键是要△AEC是等边三角形.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案
相关题目