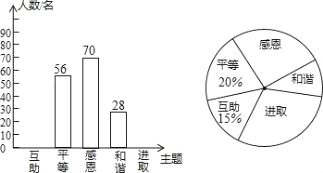
题目内容
【题目】下列命题：如图，正方形ABCD中，E、F分别为AB、AD上的点，AF=BE，CE、BF交于H，BF交AC于M，O为AC的中点，OB交CE于N，连OH．下列结论中：①BF⊥CE；②OM=ON；③ 
；④ 
．其中正确的命题有（ ）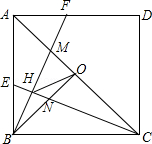 
A.只有①②
B.只有①②④
C.只有①④
D.①②③④
【答案】B
【解析】解：∵AF=BE，AB=BC，∠ABC=∠BAD=90°， ∴△ABF≌△BEC，
∴∠BCE=∠ABF，∠BFA=∠BEC，
∴△BEH∽△ABF，
∴∠BAF=∠BHE=90°，
即BF⊥EC，①正确；
∵四边形是正方形，
∴BO⊥AC，BO=OC，
由题意正方形中角ABO=角BCO，在上面所证∠BCE=∠ABF，
∴∠ECO=∠FBO，
∴△OBM≌△ONC，
∴ON=OM，
即②正确；
③∵△OBM≌△ONC，
∴BM=CN，
∵∠BOM=90°，
∴当H为BM中点时，OH= 
BM= CN（直角三角形斜边中线等于斜边的一半），
因此只有当H为BM的中点时， 
，故③错误；
④过O点作OG垂直于OH，OG交CH与G点，
在△OGC与△OHB中，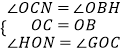
，
故△OGC≌△OHB，
∵OH⊥OG，
∴△OHG是等腰直角三角形，
按照前述作辅助线之后，OHG是等腰直角三角形，OH乘以根2之后等于HG，
则在证明证明三角形OGC与三角形OHB全等之后，CG=BH，
所以④式成立．
综上所述，①②④正确．
故选B．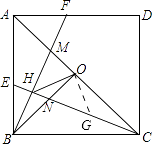
【考点精析】掌握直角三角形斜边上的中线和正方形的性质是解答本题的根本，需要知道直角三角形斜边上的中线等于斜边的一半；正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形．
