题目内容
【题目】已知,如图,∠BAG=45°,∠AGD=135°,∠E=∠F.求证:∠BAE=∠CGF. 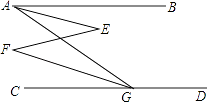
【答案】证明:∵∠BAG=45°,∠AGD=135°, ∴∠BAG+∠AGD=180°,
∴AB∥CD,
∴∠BAG=∠AGC,
∵∠E=∠F,
∴AE∥FG,
∴∠EAG=∠FGA,
∴∠BAG﹣∠EAG=∠CGA﹣∠FGA,
∴∠BAE=∠CGF
【解析】求出∠BAG+∠AGD=180°,根据平行线的判定得出AB∥CD,根据平行线的性质得出∠BAG=∠AGC,根据平行线的判定得出AE∥FG,根据平行线的性质得出∠EAG=∠FGA,即可得出答案.
【考点精析】关于本题考查的平行线的判定与性质,需要了解由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能得出正确答案.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
【题目】某校食堂的中餐与晚餐的资费标准如下:
种类 | 单价 |
米饭 | 0.5元/份 |
A类套餐菜 | 3.5元/份 |
B类套餐菜 | 2.5元/份 |
小杰同学某星期从周一到周五每天的中餐与晚餐均在学校选用A类或B类中的一份套餐菜与一份米饭用餐,这五天共消费36元.请问小杰在这五天内,A,B类套餐菜各选用了多少次?