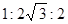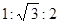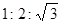题目内容
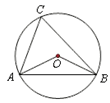
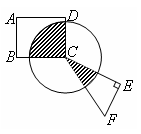
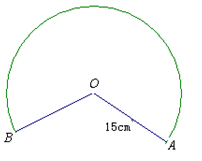
如图，若AD是⊙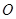
的直径，AB是⊙O的弦，∠DAB=50°，点C在圆上，则
∠ACB的度数是
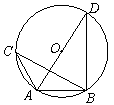
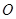的直径，AB是⊙O的弦，∠DAB=50°，点C在圆上，则∠ACB的度数是
| A．100° | B．50° | C．40° | D．20° |
C
先根据AD是⊙O的直径，得∠ABD=90°，再根据三角形的内角和定理求出∠ADB的度数，最后由圆周角定理得∠ACB．
解：∵AD是直径，
∴∠ABD=90°，
∴∠ADB=180°-∠ABD-∠DAB=40°，
∴∠ACB=∠ADB=40°．
故选C．
解：∵AD是直径，
∴∠ABD=90°，
∴∠ADB=180°-∠ABD-∠DAB=40°，
∴∠ACB=∠ADB=40°．
故选C．
练习册系列答案
相关题目
