题目内容
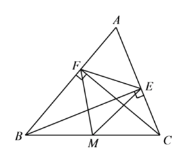
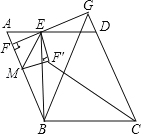
【题目】如图,平行四边形ABCD中,过点B作BE⊥AD于点E,过点E作EF⊥AB于点F,与CD的延长线交于点G,连接BG,且BE=BC,BG=5![]() ,∠BGF=45°,EG=3,若点M是线段BF上的一个动点,将△MEF沿ME所在直线翻折得到△MEF′,连接CF′,则CF′长度的最小值是_____.
,∠BGF=45°,EG=3,若点M是线段BF上的一个动点,将△MEF沿ME所在直线翻折得到△MEF′,连接CF′,则CF′长度的最小值是_____.
【答案】![]() 2
2
【解析】
连接CE,易知当点F′落在线段CE上时,线段CF′的长度最小,在△BGF中,EF⊥AB,∠BGF=45°,BG=5![]() ,可得BF=FG=5,FE=2,由勾股定理可得,BE=
,可得BF=FG=5,FE=2,由勾股定理可得,BE=![]() ,由平行四边形ABCD可得,AD∥BC,又因为BE⊥AD,推出BE⊥BC,继而推出△BCE是等腰直角三角形,然后根据勾股定理求出CE,根据翻折的性质可得EF′=EF,最后由CF′=CE-EF′即可求解.
,由平行四边形ABCD可得,AD∥BC,又因为BE⊥AD,推出BE⊥BC,继而推出△BCE是等腰直角三角形,然后根据勾股定理求出CE,根据翻折的性质可得EF′=EF,最后由CF′=CE-EF′即可求解.
解:如图所示,连接CE,易知当点F′落在线段CE上时,线段CF′的长度最小,

∵EF⊥AB,BGF=45°,BG=5![]() ,
,
∴△BGF是等腰直角三角形,BF=FG=5,
∵EG=3,
∴FE=FG- EG=5-3=2,
由勾股定理得,BE=![]() =
=![]() =
=![]() ,
,
∵四边形ABCD是平行四边形,
∴AD∥BC
又∵BE⊥AD, BE=BC
∴BE⊥BC
∴△BCE是等腰直角三角形,
由勾股定理得,CE=![]() =
=![]() ,
,
根据翻折的性质可得:EF′=EF=2,
∴CF′=CE-EF′=![]() -2
-2
故答案为:![]() -2
-2

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目