题目内容
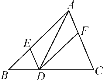
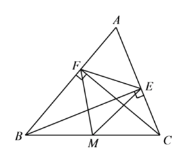
【题目】如图,在△ABC中,CF⊥AB于点F,BE⊥AC于点E,M为BC的中点连接ME、MF、EF.
(1) 求证:△MEF是等腰三角形;
(2) 若∠A=![]() ,∠ABC=50°,求∠EMF的度数.
,∠ABC=50°,求∠EMF的度数.
【答案】(1)见解析;(2)∠EMF=40°
【解析】
(1)易得△BCE和△BCF都是直角三角形,根据直角三角形斜边上的中线等于斜边的一半可得ME=MF=![]() BC,即可得证;
BC,即可得证;
(2)首先根据三角形内角和定理求出∠ACB=60°,然后由(1)可知MF=MB,ME=MC,利用等边对等角可求出∠MFB=50°,∠MEC=60°,从而推出∠BMF和∠CME的度数,即可求∠EMF的度数.
(1)∵CF⊥AB于点F,BE⊥AC于点E,
∴△BCE和△BCF为直角三角形
∵M为BC的中点
∴ME=![]() BC,MF=
BC,MF=![]() BC
BC
∴ME=MF
即△MEF是等腰三角形
(2)∵∠A=70°,∠ABC=50°,
∴∠ACB=180°-70°-50°=60°
由(1)可知MF=MB,ME=MC,
∴∠MFB=∠ABC=50°,∠MEC=∠ACB=60°,
∴∠BMF=180°-2×50°=80°,∠CME=180°-2×60°=60°
∴∠EMF=180°-∠BMF-∠CME=180°-80°-60°=40°

练习册系列答案
相关题目