题目内容
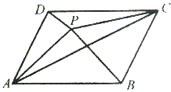
【题目】如图,点P是平行四边形ABCD内一点,已知S△PAB=7,S△PAD=4,那么S△PAC等于( )
A.4B.3.5C.3D.无法确定
【答案】C
【解析】
根据平行四边形的对边相等,可得AB=DC,再假设点P到AB的距离为h1,假设点P到DC的距离为h2,将平行四边形的面积进行分割组合,即可求解.
∵四边形ABCD是平行四边形,
∴AB=DC.
假设点P到AB的距离为h1,假设点P到DC的距离为h2,
∴S△PAB=![]() AB·h1,S△PDC=
AB·h1,S△PDC=![]() DC·h2,
DC·h2,
∴S△PAB+S△PDC=![]() ( AB·h1+DC·h2) =
( AB·h1+DC·h2) =![]() DC·(h1+h2),
DC·(h1+h2),
∵h1+h2正好是AB到DC的距离,
∴S△PAB+ S△PDC=![]() S平行四边形ABCD=S△ABC=S△ADC
S平行四边形ABCD=S△ABC=S△ADC
即S△ADC=S△PAB+ S△PDC=7+S△PDC
而S△PAC=S△ADC-S△PDC-S△PAD
∴S△PAC=7-4=3.
故选:C

练习册系列答案
相关题目