题目内容
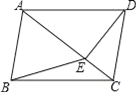
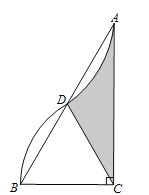
【题目】如图1,在正方形ABCD和正方形BEFG中,点A,B,E在同一条直线上,连接DF,且P是线段DF的中点,连接PG,PC.
(1)如图1中,PG与PC的位置关系是 ,数量关系是 ;
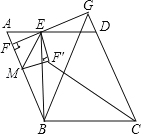
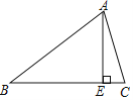
(2)如图2将条件“正方形ABCD和正方形BEFG”改为“矩形ABCD和矩形BEFG”其它条件不变,求证:PG=PC;
(3)如图3,若将条件“正方形ABCD和正方形BEFG”改为“菱形ABCD和菱形BEFG”,点A,B,E在同一条直线上,连接DF,P是线段DF的中点,连接PG、PC,且∠ABC=∠BEF=60°,求![]() 的值.
的值.

【答案】(1)PG⊥PC且PG=PC;(2)详见解析;(3)PG:PC=![]() .
.
【解析】
(1)延长GP交DC于点H,由条件可以得出△DHP≌△FGP,就可以得出DH=GF,PH=PG,根据正方形的性质就可以得出HC=GC,从而由等腰直角三角形的性质可以得出结论;
(2)如图2,延长GP交DC于点H,由条件可以得出△DHP≌△FGP,根据直角三角形的性质就可以得出结论;
(3)如图2,延长GP交DC于点H,由条件可以得出△DHP≌△FGP,根据菱形的性质可以得出△HCG是等腰三角形,由菱形的内角和可以求出∠PCG=60°,由特殊角的三角函数值就可以求出结论.
(1)PG⊥PC且PG=PC.理由:
如图1,延长GP交DC于点H.
∵四边形ABCD和BEFG是正方形,∴DC=BC,BG=GF,∠FGB=∠GCD=∠DCB=90°,∴CD∥GF,∴∠CDP=∠GFP.
∵P是线段DF的中点,∴DP=FP.
在△DHP和△FGP中,∵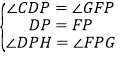 ,∴△DHP≌△FGP(ASA),∴DH=FG,PH=PG,∴HC=GC,∴△HCG是等腰直角三角形.
,∴△DHP≌△FGP(ASA),∴DH=FG,PH=PG,∴HC=GC,∴△HCG是等腰直角三角形.
∵PH=PG,∴PG⊥PC且PG=PC.
(2)如图2,延长GP交DC于点H.
∵四边形ABCD和BEFG是矩形,∴∠FGB=∠GCD=∠DCB=90°,∴CD∥GF,∴∠CDP=∠GFP.
∵P是线段DF的中点,∴DP=FP.
在△DHP和△FGP中,∵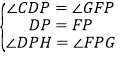 ,∴△DHP≌△FGP(ASA),∴PH=PG=
,∴△DHP≌△FGP(ASA),∴PH=PG=![]() HG.
HG.
∵∠DCB=90°,∴△HCG是直角三角形,∴CP=![]() HG,∴PG=PC;
HG,∴PG=PC;
(3)如图3,延长GP交CD于H.
∵P是DF的中点,∴DP=FP.
∵四边形ABCD和四边形BEFG是菱形,点A,B,E在同一条直线上,∴DC∥GF,∴∠HDP=∠GFP.
在△DHP和△FGP中,∵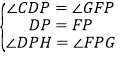 ,∴△DHP≌△FGP(ASA),∴HP=GP,DH=FG.
,∴△DHP≌△FGP(ASA),∴HP=GP,DH=FG.
∵CD=CB,FG=GB,∴CD﹣DH=CB﹣FG,即:CH=CG,∴△HCG是等腰三角形,∴PC⊥PG,∠HCP=∠GCP(等腰三角形三线合一),∴∠CPG=90°.
∵∠ABC=60°,∴∠DCB=120°,∴∠GCP=![]() ∠DCB=60°,∴Rt△CPG中,
∠DCB=60°,∴Rt△CPG中,![]() .
.
故答案为:PG⊥PC,PG=PC,PG:PC=![]() .
.