Question

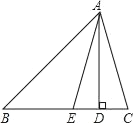
【题目】如图，在△ABC中，AD是BC边上的高，AE是∠BAC平分线．

（1）若∠B=38°，∠C=70°，求∠DAE的度数；

（2）若∠B＞∠C，试探求∠DAE、∠B、∠C之间的数量关系．

Answer 1

【答案】(1) 16°（2）∠DAE=(∠B∠C).

【解析】

（1）根据三角形内角和定理求出∠BAC，根据角平分线的定义求出∠BAE，结合图形计算即可；

（2）仿照（1）的作法计算．

(1)∵∠B=38°,∠C=70°，

∴∠BAC=72°，

∵AE是∠BAC平分线,

∴∠BAE=36°，

∵AD是BC边上的高,∠B=38°，

∴∠BAD=52°，

∴∠DAE=52°36°=16°；

(2)如图：∠BAC=180°∠B∠C，

∵AE是∠BAC平分线，

∴∠EAC=，

∠DAC=90°∠C，

∴∠DAE=90°∠C = (∠B∠C).