题目内容
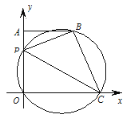
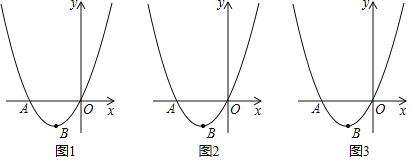
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx与x轴交于点A,顶点B的坐标为(﹣2,﹣2).
(1)求a,b的值;
(2)在y轴正半轴上取点C(0,4),在点A左侧抛物线上有一点P,连接PB交x轴于点D,连接CB交x轴于点F,当CB平分∠DCO时,求点P的坐标;
(3)在(2)的条件下,连接PC,在PB上有一点E,连接EC,若∠ECB=∠PDC,求点E的坐标.
【答案】(1)a=![]() ,b=2;(2)P(﹣6,6);(3)(﹣
,b=2;(2)P(﹣6,6);(3)(﹣![]() ,
,![]() )
)
【解析】
(1)根据顶点B的坐标及原点即可求出解析式;
(2)过点B作BH⊥y轴于点H,过点D作DG⊥CB于点G,先求出tan∠BCH=![]() ,再根据CB平分∠DCO求出点D的坐标,得到直线BD的解析式,利用抛物线的解析式即可得到点P的坐标;
,再根据CB平分∠DCO求出点D的坐标,得到直线BD的解析式,利用抛物线的解析式即可得到点P的坐标;
(3)过点P作PM⊥y轴于点M,过点B作BH⊥y轴于点H,证明△PMC≌△CHB得到∠CPB=∠CBP=45°,过点C作CN⊥CE,过点B作BN⊥BP,CN、BN交于点N,连接DN,证明△ECD≌△NCD得到DE=DN,过点P作PK⊥x轴于点K,利用勾股定理求出PD,设ED=t,作BQ⊥x轴于点Q,求出BD后根据勾股定理求出ED,作ER⊥x轴于点R,根据平行线所截线段成比例求出ER,再根据三角函数求出DR即可得到点E的坐标.
解:(1)抛物线的表达式为:y=a(x+2)2﹣2=ax2+4ax+4a﹣2,
故4a﹣2=0,
解得:a=![]() ,
,
b=4a=2;
(2)抛物线的表达式为:y=![]() x2+2x…①,
x2+2x…①,
过点B作BH⊥y轴于点H,过点D作DG⊥CB于点G,
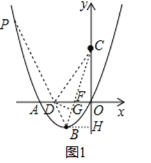
由点B、C的坐标得直线BC的表达式为:y=3x+4,则点F(﹣![]() ,0),
,0),
∵点B(﹣2,﹣2),BH=2,CH=4+2=6,则tan∠BCH=![]() =tanα,
=tanα,
∵DG⊥BC,
∴∠FDG=∠FCO=α=∠DCG,
在Rt△DFG中,设FG=m,则DG=3m,
则CG=3DG=9m,
CF=9m﹣m=8m=![]() ,
,
解得:m=![]() ,
,
DF=![]() ,
,
OD=OF+DF=3,故点D(﹣3,0),
由点B、D的坐标可得,直线PB的表达式为:y=﹣2x﹣6…②,
联立①②并解得:x=﹣2(舍去)或﹣6,
故点P(﹣6,6);
(3)如图2,过点P作PM⊥y轴于点M,过点B作BH⊥y轴于点H,
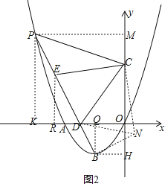
∵P(﹣6,6),
则PM=OM=6,
∴CM=2,PM=CH,
∴BH=CM,
∵∠PMC=∠BHC=90°,
∴△PMC≌△CHB(HL),
∴CP=CB,∠MPC=∠BCH,
∵∠MPC+∠PCM=90°,
∴∠BCH+∠PCM=90°,
∴∠PCB=90°,
∴∠CPB=∠CBP=45°,
过点C作CN⊥CE,过点B作BN⊥BP,CN、BN交于点N,连接DN,
则∠CBN=90°﹣∠CPB=45°,
∴∠CPB=∠CBN,
∵∠ECN=∠EBN=90°,
∴∠CEB+∠CNB=180°,
∵∠CEB+∠PEC=180°,
∴∠CNB=∠PEC,
∵PC=CB,
∴△PEC≌△BNC(SAS),
则PE=BN,CE=CN,
∵∠ECB=∠EDC+∠DCB,∠PDC=∠DCB+∠CBD,∠ECB=∠PDC,
∴∠ECD=∠CBD=45°,
∴∠DCN=90°﹣∠ECD=45°,
∴∠ECD=∠DCN,
∵CD=CD,
∴△ECD≌△NCD(SAS),
∴DE=DN,
在Rt△DBN中,BD2+BN2=DN2,则BD2+PE2=DE2,
过点P作PK⊥x轴于点K,
∴PK=KO=6,
∵OD=3,
∴KD=3,
在Rt△PKD中,PD=![]() ,
,
设ED=t,则PE=3![]() ﹣t,
﹣t,
过点B作BQ⊥x轴于点Q,则BQ=OQ=2,DQ=OD﹣OQ=1,
在Rt△BDQ中,BD=![]() =
=![]() ,
,
故(![]() )2+(3
)2+(3![]() ﹣t)2=t2,
﹣t)2=t2,
解得:t=![]() ,
,
故DE=![]() ,
,
过点E作ER⊥x轴于点R,则ER∥PK,
故![]() ,即
,即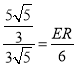 ,
,
解得:ER=![]()
∵∠EDR=∠BDQ,
故tan∠EDR=tan∠BDQ,
即:![]() =2,
=2,
故DR=![]() ,OR=DR+OD=
,OR=DR+OD=![]() +3=
+3=![]() ,
,
故点E的坐标为:(﹣![]() ,
,![]() ).
).

 教材全解字词句篇系列答案
教材全解字词句篇系列答案