��Ŀ����
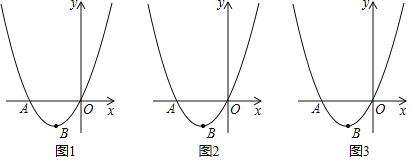
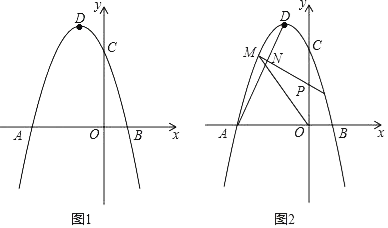
����Ŀ�� ��ͼ1����֪ˮ��ͷ��ˮ�ij�ʼ�ٶ�v0���Էֽ�Ϊ�����ʼ�ٶ�vx�������ʼ�ٶ�vy������ˮ��ͷ�����ǣ���v02=vx2+vy2��ͼ2��һ������б���ϵĻ��Գ��صĽ���ʾ��ͼ��ˮ��ͷ�������A��ɽ�µ��¶��ϣ�����������߶Ⱥ��Բ��ƣ����¶���Ǧֱ�߶�OAΪ15�ף�ɽ�µ��±�Ϊ![]() ���뿪ˮ��ͷ���ˮ�����ɵ㣩��ó�ʼ�ٶ�v0��/�����˶�·�����Կ����������ߣ���M���˶������е�ijһλ�ã����Կ���������ʵ�������M��A�ĸ߶�֮��d���ף������ʱ��t���룩�Ĺ�ϵΪd=vyt-5t2��M��A��ˮƽ����Ϊvxt�ף���֪��ˮ���ij�ʼ�ٶ�v0Ϊ15��/�룬ˮ��ͷ��������Ϊ53����
���뿪ˮ��ͷ���ˮ�����ɵ㣩��ó�ʼ�ٶ�v0��/�����˶�·�����Կ����������ߣ���M���˶������е�ijһλ�ã����Կ���������ʵ�������M��A�ĸ߶�֮��d���ף������ʱ��t���룩�Ĺ�ϵΪd=vyt-5t2��M��A��ˮƽ����Ϊvxt�ף���֪��ˮ���ij�ʼ�ٶ�v0Ϊ15��/�룬ˮ��ͷ��������Ϊ53����

��1����ˮ���ĺ����ʼ�ٶ�vx�������ʼ�ٶ�vy��
��2���ú�t�Ĵ���ʽ��ʾ��M�ĺ�����x��������y������y��x�Ĺ�ϵʽ����дx��ȡֵ��Χ����
��3��ˮ����ɽ���ϵ����C�������A��ˮƽ�����Ƕ����ף���Ҫʹˮ��ǡ�����䵽�½�B����С��������ͬ�����£�����Ҫ�������A������AB�����ƶ������ף����ο����ݣ�sin53���![]() ��cos53���
��cos53���![]() ��tan53���
��tan53���![]() ��
��
���𰸡���1��ˮ���ĺ����ʼ�ٶ�vx��9��/�룬�����ʼ�ٶ�vy��12��/�룻��2��y=-![]() +
+![]() x+15����3��ˮ����ɽ���ϵ����C�������A��ˮƽ������27�ף���Ҫ�������A������AB�����ƶ�
x+15����3��ˮ����ɽ���ϵ����C�������A��ˮƽ������27�ף���Ҫ�������A������AB�����ƶ�![]() ��
��
��������
��1���������������������Һ����Ҷ���ɵý��ۣ�
��2���ɣ�1���ı�ʾ��vx��ʾ��x��OA��֪������y=d+OA������OA��ֵ��d��t�ĺ�����ϵʽ�����Եý⣻
��3������õ�A�͵�B�����꣬����д����ֱ�߽���ʽ���ٽ����루2���������߽���ʽ�������Ӷ�������C�����꣬������ƽ��֪ʶ�����ɶ���������⣮
�⣺��1����v0Ϊ15��/�룬ˮ��ͷ��������Ϊ53����
��cos��=![]() ��sin��=
��sin��=![]() ��
��
��vx=15cos53��=15��![]() =9��vy=15sin53��=15��
=9��vy=15sin53��=15��![]() =12��
=12��
��ˮ���ĺ����ʼ�ٶ�vx��9��/�룬�����ʼ�ٶ�vy��12��/�룻
��2��x=vxt=9t��
��t=![]() ��
��
��M��A�ĸ߶�֮��d���ף������ʱ��t���룩�Ĺ�ϵΪd=vyt-5t2
��y=d+OA=12t-5t2+15=-5��![]() +12��
+12��![]() +15=-
+15=-![]() +
+![]() x+15��
x+15��
��y��x�Ĺ�ϵʽΪ��y=-![]() +
+![]() x+15��
x+15��
��3�����¶���Ǧֱ�߶�OAΪ15�ף�ɽ�µ��±�Ϊ![]() ��
��
��OB=45�ף���A��0��15����B��45��0��
��ֱ��AB�Ľ���ʽΪ��y=![]() +15�������������߽���ʽ�����ã�
+15�������������߽���ʽ�����ã�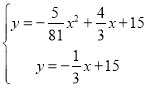 ��
��
���![]() ���ᣩ��
���ᣩ��![]() ��
��
��ˮ����ɽ���ϵ����C����Ϊ��27��6���������A������AB�����ƶ��ľ������BC�ľ��룬
��BC=![]() =
=![]() �ף�
�ף�
��ˮ����ɽ���ϵ����C�������A��ˮƽ������27�ף���Ҫ�������A������AB�����ƶ�![]() �ף�
�ף�

 �Ķ��쳵ϵ�д�
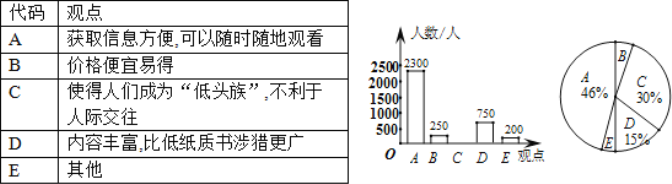
�Ķ��쳵ϵ�д�����Ŀ��ij��˾����Ͳ�����������ʽ��������Ա�����ʶ�ȡ�ͣ������˷����ù�˾����10�����ţ��Ҹ����ŵ�������ͬ.Ϊ�˽���͵��˷����������10�������������ȡ��![]() �������ţ��������������ܣ�20�������գ��ĵ��飬�õ�����������ÿ������˷ѷ��˵����������¼����ÿ�ղ�������������λ��ǧ�ˣ���������Щ���ݽ����������������ͷ���.��������˲�����Ϣ.
�������ţ��������������ܣ�20�������գ��ĵ��飬�õ�����������ÿ������˷ѷ��˵����������¼����ÿ�ղ�������������λ��ǧ�ˣ���������Щ���ݽ����������������ͷ���.��������˲�����Ϣ.![]() .
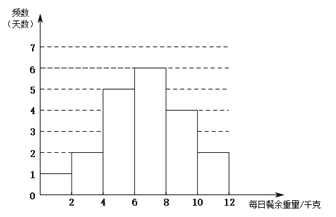
.![]() ����ÿ�ղ���������Ƶ���ֲ�ֱ��ͼ���£����ݷֳ�6�飺
����ÿ�ղ���������Ƶ���ֲ�ֱ��ͼ���£����ݷֳ�6�飺![]() ��
��![]() ��
��![]() ��
��![]() ����
����
![]() .
.![]() ����ÿ�ղ���������
����ÿ�ղ���������![]() ��һ����ǣ�6.1 6.6 7.0 7.0 7.0 7.8
��һ����ǣ�6.1 6.6 7.0 7.0 7.0 7.8
![]() .
.![]() ����ÿ�ղ����������£�1.4 2.8 6.9 7.8 1.9 9.7 3.1 4.6 6.9 10.8 6.9 2.6 7.5 6.9 9.5 7.8 8.4 8.3 9.4 8.8
����ÿ�ղ����������£�1.4 2.8 6.9 7.8 1.9 9.7 3.1 4.6 6.9 10.8 6.9 2.6 7.5 6.9 9.5 7.8 8.4 8.3 9.4 8.8
![]() .
. ![]() ����������20��������ÿ�ղ���������ƽ��������λ�����������£�
����������20��������ÿ�ղ���������ƽ��������λ�����������£�
���� | ƽ���� | ��λ�� | ���� |
| 6.4 | | 7.0 |
| 6.6 | 7.2 | |
����������Ϣ���ش��������⣺
��1��д����![]() �е�ֵ��
�е�ֵ��
��2����![]() �����������У����ʶ�ȡ�ͣ������˷������ýϺõIJ�����________������
�����������У����ʶ�ȡ�ͣ������˷������ýϺõIJ�����________������![]() ������
������![]() ������������____________��
������������____________��
��3�����![]() ����������ÿ�ղ������������ݣ����Ƹù�˾��10�����ţ�һ�꣨��240�������ռ��㣩�IJ���������.
����������ÿ�ղ������������ݣ����Ƹù�˾��10�����ţ�һ�꣨��240�������ռ��㣩�IJ���������.