题目内容
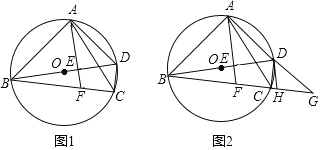
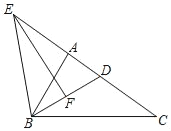
【题目】已知：如图，在△ABC中，点D在边AC上，BD的垂直平分线交CA的延长线于点E，交BD于点F，联结BE，ED2＝EAEC．
（1）求证：∠EBA＝∠C；
（2）如果BD＝CD，求证：AB2＝ADAC．
【答案】（1）证明见解析；（2）证明见解析.
【解析】
（1）欲证明∠EBA=∠C，只要证明△BAE∽△CEB即可；
（2）欲证明AB2=ADAC，只要证明△BAD∽△CAB即可．
（1）∵ED2=EAEC，∴
．
∵∠BEA=∠CEB，∴△BAE∽△CBE，∴∠EBA=∠C．
（2）∵EF垂直平分线段BD，∴EB=ED，∴∠EDB=∠EBD，∴∠C+∠DBC=∠EBA+∠ABD．
∵∠EBA=∠C，∴∠DBC=∠ABD．
∵DB=DC，∴∠C=∠DBC，∴∠ABD=∠C．
∵∠BAD=∠CAB，∴△BAD∽△CAB，∴
，∴AB2=ADAC．
练习册系列答案
相关题目
【题目】某同学在利用描点法画二次函数y＝ax2+bx+c（a＝0）的图象时，先取自变量x的一些值，计算出相应的函数值y，如下表所示：
x | … | 0 | 1 | 2 | 3 | 4 | … |
y | … | ﹣3 | 0 | ﹣1 | 0 | 3 | … |
接着，他在描点时发现，表格中有一组数据计算错误，他计算错误的一组数据是（ ）
A.
B.
C.
D.
