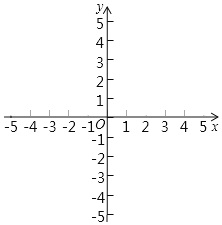Question

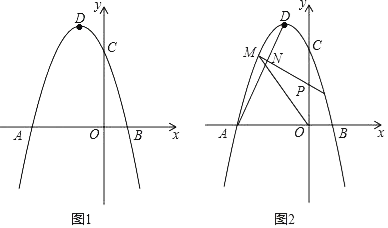
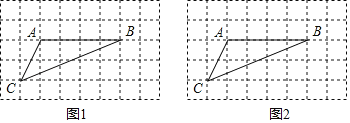
【题目】如图，在8×5的正方形网格中，每个小正方形的边长均为1，△ABC的三个顶点均在小正方形的顶点上．

（1）在图1中画出△ABD（点D在小正方形的顶点上），使△ABD的周长等于△ABC的周长，且四边形ACBD是中心对称图形；

（2）在图2中找一点E（点E在小正方形的顶点上），使tan∠AEB＝2（AE＜EB），且四边形ACEB的对边不平行，并直接写出图2中四边形ACEB的面积．

Answer 1

【答案】（1）见解析；（2）画图见解析，8.5

【解析】

（1）根据中心对称图形的特点画图即可；

（2）根据等腰直角三角形的性质，全等三角形及相似三角形的性质即可画出图形，利用面积相加的关系列式求出四边形ACEB的面积.

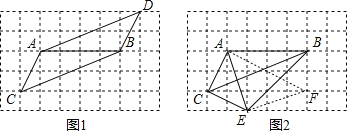
解：（1）如图，△ABD即为所求．

（2）如图，四边形ABEC即为所求．

四边形ACEB的面积＝××+×4×3＝8.5．