Question

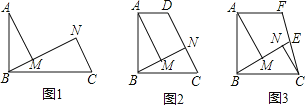
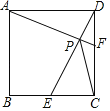
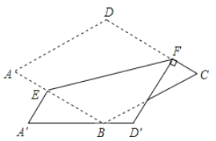
【题目】如图，在菱形纸片中，，将纸片折叠，点分别落在点处，且经过点为折痕，当时，的值为( )

A.B.C.D.

Answer 1

【答案】A

【解析】

首先延长DC与AD，交于点M，由四边形ABCD是菱形与折叠的性质，易求得△BCM是等腰三角形，△DFM是含30°角的直角三角形，然后设CF=x，DF=DF=y，利用正切函数的知识，即可求得答案.

解：延长DC与AD，交于点M

∵在菱形纸片ABCD中，∠A=60°

∴∠DCB=∠A=60°

∵AB∥CD

∴∠D=180°-∠A=120°

根据折叠的性质，可得∠ADF=∠D=120°

∴∠FDM=180°-∠ADF=60°

∵DF⊥CD

∴∠DFM=90°，∠M=90°-∠FDM=30°

∵∠BCM=180°-∠BCD=120°

∴∠CBM=180°-∠BCM-∠M=30°

∴∠CBM=∠M=30°

∴BC=CM

设CF=x，DF=DF=y

则BC=CM=CD=CF+DF=x+y

∴FM=CM+CF=2x+y

在Rt△DFM中，tanM=tan30°=

∴x=y

∴=

故选A.